Communications Toolbox

Creating and Decoding Reed-Solomon Codes

The rsenc and rsdec functions create and decode Reed-Solomon codes, using the data described in Representing Words for Reed-Solomon Codes and Parameters for Reed-Solomon Codes.

This section illustrates how to use rsenc and rsdec. The topics are

• Example: Reed-Solomon Coding Syntaxes
• Example: Detecting and Correcting Errors
• Excessive Noise in Reed-Solomon Codewords
• Creating Shortened Reed-Solomon Codes

Example: Reed-Solomon Coding Syntaxes

The example below illustrates multiple ways to encode and decode data using a [15,13] Reed-Solomon code. The example shows that you can

• Vary the generator polynomial for the code, using rsgenpoly to produce a different generator polynomial
• Vary the primitive polynomial for the Galois field that contains the symbols, using an input argument in gf.
• Vary the position of the parity symbols within the codewords, choosing either the end (default) or beginning

The example also shows that corresponding syntaxes of rsenc and rsdec use the same input arguments, except for the first input argument.

• m = 4; % Number of bits in each symbol
  n = 2^m-1; k = 13; % Codeword length and message length
  data = randint(4,k,2^m); % Four random integer messages
  msg = gf(data,m); % Represent data using a Galois array.
  
  % Simplest syntax for encoding
  c1 = rsenc(msg,n,k);
  d1 = rsdec(c1,n,k);
  
  % Vary the generator polynomial for the code.
  c2 = rsenc(msg,n,k,rsgenpoly(n,k,19,2));
  d2 = rsdec(c2,n,k,rsgenpoly(n,k,19,2));
  
  % Vary the primitive polynomial for GF(16).
  msg2 = gf(data,m,25);
  c3 = rsenc(msg2,n,k);
  d3 = rsdec(c3,n,k);
  
  % Prepend the parity symbols instead of appending them.
  c4 = rsenc(msg,n,k,'beginning');
  d4 = rsdec(c4,n,k,'beginning');
  
  % Check that the decoding worked correctly.
  chk = isequal(d1,msg) & isequal(d2,msg) & isequal(d3,msg2) &...
  isequal(d4,msg)
  
  chk =
  
       1
  

Example: Detecting and Correcting Errors

The example below illustrates the decoding results for a corrupted code. The example encodes some data, introduces errors in each codeword, and invokes rsdec to attempt to decode the noisy code. It uses additional output arguments in rsdec to gain information about the success of the decoding process.

• m = 3; % Number of bits per symbol
  n = 2^m-1; k = 3; % Codeword length and message length
  t = (n-k)/2; % Error-correction capability of the code
  nw = 4; % Number of words to process
  msgw = gf(randint(nw,k,2^m),m); % Random k-symbol messages
  c = rsenc(msgw,n,k); % Encode the data.
  noise = (1+randint(nw,n,2^m-1)).*randerr(nw,n,t); % t errors/row
  cnoisy = c + noise; % Add noise to the code.
  [dc,nerrs,corrcode] = rsdec(cnoisy,n,k); % Decode the noisy code.
  % Check that the decoding worked correctly.
  isequal(dc,msgw) & isequal(corrcode,c)
  nerrs % Find out how many errors rsdec corrected.
  

Notice that the array of noise values contains integers between 1 and 2^m, and that the addition operation c + noise takes place in the Galois field GF(2^m) because c is a Galois array in GF(2^m).

The output from the example is below. The nonzero value of ans indicates that the decoder was able to correct the corrupted codewords and recover the original message. The values in the vector nerrs indicates that the decoder corrected t errors in each codeword.

• ans =
  
       1
  
  
  nerrs =
  
       2
       2
       2
       2
  

Excessive Noise in Reed-Solomon Codewords

In the previous example, rsdec corrected all of the errors. However, each Reed-Solomon code has a finite error-correction capability. If the noise is so great that the corrupted codeword is too far in Hamming distance from the correct codeword, then either

• The corrupted codeword is close to a valid codeword other than the correct codeword. The decoder returns the message that corresponds to the other codeword.
• The corrupted codeword is not close enough to any codeword for successful decoding. This situation is called a decoding failure. The decoder removes the symbols in parity positions from the corrupted codeword and returns the remaining symbols.

In both cases, the decoder returns the wrong message. However, you can tell when a decoding failure occurs because rsdec also returns a value of -1 in its second output.

To examine cases in which codewords are too noisy for successful decoding, change the previous example so that the definition of noise is

• noise = (1+randint(nw,n,n)).*randerr(nw,n,t+1); % t+1 errors/row
  

Creating Shortened Reed-Solomon Codes

Every Reed-Solomon encoder uses a codeword length that equals 2^m-1 for an integer m. A shortened Reed-Solomon code is one in which the codeword length is not 2^m-1. A shortened [n,k] Reed-Solomon code implicitly uses an [n₁,k₁] encoder, where

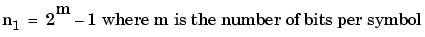
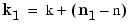
The rsenc and rsdec functions support shortened codes using the same syntaxes that they use for nonshortened codes. You do not need to indicate explicitly that you want to use a shortened code. For example, compare the two similar-looking commands below. The first creates a (nonshortened) [7,5] code. The second causes rsenc to create a [5,3] shortened code by implicitly using a [7,5] encoder.

• m = 3; ordinarycode = rsenc(gf([1 1 1 1 1],m),7,5);
  m = 3; shortenedcode = rsenc(gf([1 1 1],m),5,3);
  

How rsenc Creates a Shortened Code.   When creating a shortened code, rsenc performs these steps:

• Pads each message by prepending zeros
• Encodes each padded message using a Reed-Solomon encoder having an allowable codeword length and the desired error-correction capability
• Removes the extra zeros from the nonparity symbols of each codeword

The example below illustrates this process. Note that forming a [12,8] Reed-Solomon code actually uses a [15,11] Reed-Solomon encoder. Also note that you do not have to indicate in the rsenc syntax that this is a shortened code or that the proper encoder to use is [15,11].

• n = 12; k = 8; % Lengths for the shortened code
  m = ceil(log2(n+1)); % Number of bits per symbol
  msg = gf(randint(3,k,2^m),m); % Random array of 3 k-symbol words
  code = rsenc(msg,n,k); % Create a shortened code.
  
  % Do the shortening manually, just to show how it works.
  n_pad = 2^m-1; % Codeword length in the actual encoder
  k_pad = k+(n_pad-n); % Message length in the actual encoder
  msg_pad=[zeros(3, n_pad-n), msg]; % Prepend zeros to each word.
  code_pad = rsenc(msg_pad,n_pad,k_pad); % Encode padded words.
  code_eqv = code_pad(:,n_pad-n+1:n_pad); % Remove extra zeros.
  ck = isequal(code_eqv,code); % Returns true (1).
  

Parameters for Reed-Solomon Codes

Selected Bibliography for Block Coding