Communications Toolbox

hilbiir

Design a Hilbert transform IIR filter

Syntax

• hilbiir;
  hilbiir(ts);
  hilbiir(ts,dly);
  hilbiir(ts,dly,bandwidth);
  hilbiir(ts,dly,bandwidth,tol);
  [num,den] = hilbiir(...);
  [num,den,sv] = hilbiir(...);
  [a,b,c,d] = hilbiir(...);
  [a,b,c,d,sv] = hilbiir(...);
  

Description

The function hilbiir designs a Hilbert transform filter. The output is either

• A plot of the filter's impulse response, or
• A quantitative characterization of the filter, using either a transfer function model or a state-space model

Background Information

An ideal Hilbert transform filter has the transfer function H(s) = -jsgn(s), where sgn(.) is the signum function (sign in MATLAB). The impulse response of the Hilbert transform filter is

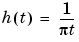
Because the Hilbert transform filter is a noncausal filter, the hilbiir function introduces a group delay, dly. A Hilbert transform filter with this delay has the impulse response

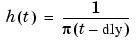
Choosing a Group Delay Parameter

The filter design is an approximation. If you provide the filter's group delay as an input argument, then these two suggestions can help improve the accuracy of the results:

• Choose the sample time ts and the filter's group delay dly so that dly is at least a few times larger than ts and rem(dly,ts) = ts/2. For example, you can set ts to 2*dly/N, where N is a positive integer.
• At the point t = dly, the impulse response of the Hilbert transform filter can be interpreted as 0, -Inf, or Inf. If hilbiir encounters this point, then it sets the impulse response there to zero. To improve accuracy, avoid the point t = dly.

Syntaxes for Plots

Each of these syntaxes produces a plot of the impulse response of the filter that the hilbiir function designs, as well as the impulse response of a corresponding ideal Hilbert transform filter.

hilbiir plots the impulse response of a fourth-order digital Hilbert transform filter with a 1-second group delay. The sample time is 2/7 seconds. In this particular design, the tolerance index is 0.05. The plot also displays the impulse response of the ideal Hilbert transform filter with a 1-second group delay.

hilbiir(ts) plots the impulse response of a fourth-order Hilbert transform filter with a sample time of ts seconds and a group delay of ts*7/2 seconds. The tolerance index is 0.05. The plot also displays the impulse response of the ideal Hilbert transform filter having a sample time of ts seconds and a group delay of ts*7/2 seconds.

hilbiir(ts,dly) is the same as the syntax above, except that the filter's group delay is dly for both the ideal filter and the filter that hilbiir designs. See Choosing a Group Delay Parameter above for guidelines on choosing dly.

hilbiir(ts,dly,bandwidth) is the same as the syntax above, except that bandwidth specifies the assumed bandwidth of the input signal and that the filter design might use a compensator for the input signal. If bandwidth = 0 or bandwidth > 1/(2*ts), then hilbiir does not use a compensator.

hilbiir(ts,dly,bandwidth,tol) is the same as the syntax above, except that tol is the tolerance index. If tol < 1, then the order of the filter is determined by

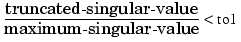
If tol > 1, then the order of the filter is tol.

Syntaxes for Transfer Function and State-Space Quantities

Each of these syntaxes produces quantitative information about the filter that hilbiir designs, but does not produce a plot. The input arguments for these syntaxes (if you provide any) are the same as those described in the Syntaxes for Plots section above.

[num,den] = hilbiir(...) outputs the numerator and denominator of the IIR filter's transfer function.

[num,den,sv] = hilbiir(...) outputs the numerator and denominator of the IIR filter's transfer function, and the singular values of the Hankel matrix that hilbiir uses in the computation.

[a,b,c,d] = hilbiir(...) outputs the discrete-time state-space model of the designed Hilbert transform filter. a, b, c, and d are matrices.

[a,b,c,d,sv] = hilbiir(...) outputs the discrete-time state-space model of the designed Hilbert transform filter, and the singular values of the Hankel matrix that hilbiir uses in the computation.

Algorithm

The hilbiir function calculates the impulse response of the ideal Hilbert transform filter response with a group delay. It fits the response curve using a singular-value decomposition method. See the book by Kailath listed below.

Examples

At the MATLAB prompt, type hilbiir or [num,den] = hilbiir for an example using the function's default values.

See Also

grpdelay

References

Kailath, Thomas, Linear Systems, Englewood Cliffs, N.J., Prentice-Hall, 1980.

hank2sys

ifft