Communications Toolbox

Representing Elements of Galois Fields

This section describes how to create a Galois array, which is a MATLAB expression that represents elements of a Galois field. This section also describes how MATLAB interprets the numbers that you use in the representation, and includes several examples. The topics are

• Creating a Galois Array
• Example: Creating Galois Field Variables
• Example: Representing Elements of GF(8)
• How Integers Correspond to Galois Field Elements
• Example: Representing a Primitive Element

Creating a Galois Array

To begin working with data from a Galois field GF(2^m), you must set the context by associating the data with crucial information about the field. The gf function performs this association and creates a Galois array in MATLAB. This function accepts as inputs

• The Galois field data, x, which is a MATLAB array whose elements are integers between 0 and 2^m-1.
• (Optional) An integer, m, that indicates that x is in the field GF(2^m). Valid values of m are between 1 and 16. The default is 1, which means that the field is GF(2).
• (Optional) A positive integer that indicates which primitive polynomial for GF(2^m) you are using in the representations in x. If you omit this input argument, then gf uses a default primitive polynomial for GF(2^m). For information about this argument, see Specifying the Primitive Polynomial.

The output of the gf function is a variable that MATLAB recognizes as a Galois field array, rather than an array of integers. As a result, when you manipulate the variable, MATLAB works within the Galois field you have specified. For example, if you apply the log function to a Galois array, then MATLAB computes the logarithm in the Galois field and not in the field of real or complex numbers.

When MATLAB Implicitly Creates a Galois Array.   Some operations on Galois arrays require multiple arguments. If you specify one argument that is a Galois array and another that is an ordinary MATLAB array, then MATLAB interprets both as Galois arrays in the same field. That is, it implicitly invokes the gf function on the ordinary MATLAB array. This implicit invocation simplifies your syntax because you can omit some references to the gf function. For an example of the simplification, see Example: Addition and Subtraction.

Example: Creating Galois Field Variables

The code below creates a row vector whose entries are in the field GF(4), and then adds the row to itself.

• x = 0:3; % A row vector containing integers
  m = 2; % Work in the field GF(2^2), or, GF(4).
  a = gf(x,m) % Create a Galois array in GF(2^m).
  b = a + a % Add a to itself, creating b.
  

The output is

• a = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
   
  Array elements = 
   
       0     1     2     3
  
  
  b = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
   
  Array elements = 
   
       0     0     0     0
  

The output shows the values of the Galois arrays named a and b. Notice that each output section indicates

• The field containing the variable, namely, GF(2^2) = GF(4).
• The primitive polynomial for the field. In this case, it is the toolbox's default primitive polynomial for GF(4).
• The array of Galois field values that the variable contains. In particular, the array elements in a are exactly the elements of the vector x, while the array elements in b are four instances of the zero element in GF(4).

The command that creates b shows how, having defined the variable a as a Galois array, you can add a to itself by using the ordinary + operator. MATLAB performs the vectorized addition operation in the field GF(4). Notice from the output that

• Compared to a, b is in the same field and uses the same primitive polynomial. It is not necessary to indicate the field when defining the sum, b, because MATLAB remembers that information from the definition of the addends, a.
• The array elements of b are zeros because the sum of any value with itself, in a Galois field of characteristic two, is zero. This result differs from the sum x + x, which represents an addition operation in the infinite field of integers.

Example: Representing Elements of GF(8)

To illustrate what the array elements in a Galois array mean, the table below lists the elements of the field GF(8) as integers and as polynomials in a primitive element, A. The table should help you interpret a Galois array like

• gf8 = gf([0:7],3); % Galois vector in GF(2^3)
  

Integer Representation	Binary Representation	Element of GF(8)
0	000	0
1	001	1
2	010	A
3	011	A + 1
4	100	A2
5	101	A2 + 1
6	110	A2 + A
7	111	A2 + A + 1

How Integers Correspond to Galois Field Elements

Building on the GF(8) example above, this section explains the interpretation of array elements in a Galois array in greater generality. The field GF(2^m) has 2^m distinct elements, which this toolbox labels as 0, 1, 2,..., 2^m-1. These integer labels correspond to elements of the Galois field via a polynomial expression involving a primitive element of the field. More specifically, each integer between 0 and 2^m-1 has a binary representation in m bits. Using the bits in the binary representation as coefficients in a polynomial, where the least significant bit is the constant term, leads to a binary polynomial whose order is at most m-1. Evaluating the binary polynomial at a primitive element of GF(2^m) leads to an element of the field.

Conversely, any element of GF(2^m) can be expressed as a binary polynomial of order at most m-1, evaluated at a primitive element of the field. The m-tuple of coefficients of the polynomial corresponds to the binary representation of an integer between 0 and 2^m.

Below is a symbolic illustration of the correspondence of an integer X, representable in binary form, with a Galois field element. Each b_k is either zero or one, while A is a primitive element.

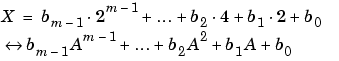
Example: Representing a Primitive Element

The code below defines a variable alph that represents a primitive element of the field GF(2⁴).

• m = 4; % Or choose any positive integer value of m.
  alph = gf(2,m) % Primitive element in GF(2^m)
  

The output is

• alph = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
   
  Array elements = 
   
       2
  

The Galois array alph represents a primitive element because of the correspondence between

• The integer 2, specified in the gf syntax
• The binary representation of 2, which is 10 (or 0010 using four bits)
• The polynomial A + 0, where A is a primitive element in this field (or 0A³ + 0A² + A + 0 using the four lowest powers of A)

Galois Field Terminology

Primitive Polynomials and Element Representations