MATLAB Function Reference

legendre

Associated Legendre functions

Syntax

• P = legendre(n,X)
  S = legendre(n,X,'sch')
  N = legendre(n,X,'norm')
  

Definitions

Associated Legendre Functions.   The Legendre functions are defined by

where

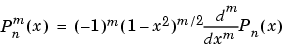
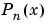
is the Legendre polynomial of degree .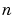

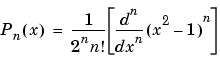
Schmidt Seminormalized Associated Legendre Functions.   The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions 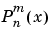by

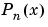
• for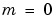

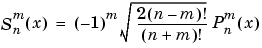
• for .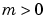

Fully Normalized Associated Legendre Functions.   The fully normalized associated Legendre functions are normalized such that

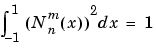
and are related to the unnormalized associated Legendre functions 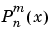by

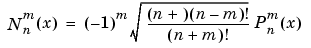
Description

P = legendre(n,X) computes the associated Legendre functions 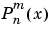of degree n and order m = 0,1,...,n, evaluated for each element of X. Argument n must be a scalar integer, and X must contain real values in the domain .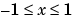

If X is a vector, then P is an (n+1)-by-q matrix, where q = length(X). Each element P(m+1,i) corresponds to the associated Legendre function of degree n and order m evaluated at X(i).

In general, the returned array P has one more dimension than X, and each element P(m+1,i,j,k,...) contains the associated Legendre function of degree n and order m evaluated at X(i,j,k,...). Note that the first row of P is the Legendre polynomial evaluated at X, i.e., the case where m = 0.

S = legendre(n,X,'sch') computes the Schmidt seminormalized associated Legendre functions .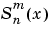

N = legendre(n,X,'norm') computes the fully normalized associated Legendre functions .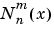

Examples

Example 1. The statement legendre(2,0:0.1:0.2) returns the matrix

	x = 0	x = 0.1	x = 0.2
m = 0	-0.5000	-0.4850	-0.4400
m = 1	0	-0.2985	-0.5879
m = 2	3.0000	2.9700	2.8800

Example 2. Given,

• X = rand(2,4,5); 
  n = 2;
  P = legendre(n,X) 
  

then

• size(P)
  ans =
       3     2     4     5
  

and

• P(:,1,2,3)
  ans =
     -0.2475
     -1.1225
      2.4950
  

is the same as

• legendre(n,X(1,2,3))
  ans =
     -0.2475
     -1.1225
      2.4950
  

Algorithm

legendre uses a three-term backward recursion relationship in m. This recursion is on a version of the Schmidt seminormalized associated Legendre functions 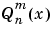, which are complex spherical harmonics. These functions are related to the standard Abramowitz and Stegun [1] functions 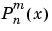by

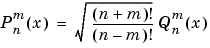
They are related to the Schmidt form given previously by

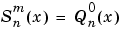
for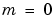

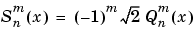
• for .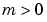

References

[1]  Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, Dover Publlications, 1965, Ch.8.

[2]  Jacobs, J. A., Geomagnetism, Academic Press, 1987, Ch.4.

legend

length