MATLAB Function Reference

fminbnd

Minimize a function of one variable on a fixed interval

Syntax

• x = fminbnd(fun,x1,x2)
  x = fminbnd(fun,x1,x2,options)
  x = fminbnd(fun,x1,x2,options,P1,P2,...)
  [x,fval] = fminbnd(...)
  [x,fval,exitflag] = fminbnd(...)
  [x,fval,exitflag,output] = fminbnd(...)
  

Description

fminbnd finds the minimum of a function of one variable within a fixed interval.

x = fminbnd(fun,x1,x2) returns a value x that is a local minimizer of the function that is described in fun in the interval x1 <= x <= x2.

x = fminbnd(fun,x1,x2,options) minimizes with the optimization parameters specified in the structure options. You can define these parameters using the optimset function. fminbnd uses these options structure fields:

Display	Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' displays just the final output; 'notify' (default) dislays output only if the function does not converge.
MaxFunEvals	Maximum number of function evaluations allowed.
MaxIter	Maximum number of iterations allowed.
TolX	Termination tolerance on x.

x = fminbnd(fun,x1,x2,options,P1,P2,...) provides for additional arguments, P1, P2, etc., which are passed to the objective function, fun(x,P1,P2,...). Use options=[] as a placeholder if no options are set.

[x,fval] = fminbnd(...) returns the value of the objective function computed in fun at x.

[x,fval,exitflag] = fminbnd(...) returns a value exitflag that describes the exit condition of fminbnd:

>0	Indicates that the function converged to a solution x.
0	Indicates that the maximum number of function evaluations was exceeded.
<0	Indicates that the function did not converge to a solution.

[x,fval,exitflag,output] = fminbnd(...) returns a structure output that contains information about the optimization:

output.algorithm	The algorithm used
output.funcCount	The number of function evaluations
output.iterations	The number of iterations taken

Arguments

fun is the function to be minimized. fun accepts a scalar x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle.

• x = fminbnd(@myfun,x0)
  

where myfun is a MATLAB function such as

• function f = myfun(x)
  f = ...         % Compute function value at x.
  

fun can also be an inline object.

• x = fminbnd(inline('sin(x*x)'),x0);
  

Other arguments are described in the syntax descriptions above.

Examples

x = fminbnd(@cos,3,4) computes 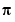to a few decimal places and gives a message on termination.

• [x,fval,exitflag] =
     fminbnd(@cos,3,4,optimset('TolX',1e-12,'Display','off'))
  

computes 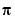to about 12 decimal places, suppresses output, returns the function value at x, and returns an exitflag of 1.

The argument fun can also be an inline function. To find the minimum of the function 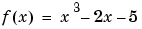on the interval (0,2), create an inline object f

• f = inline('x.^3-2*x-5');
  

Then invoke fminbnd with

• x = fminbnd(f, 0, 2)
  

The result is

• x =
      0.8165
  

The value of the function at the minimum is

• y = f(x)
  
  y =
      -6.0887
  

Algorithm

The algorithm is based on Golden Section search and parabolic interpolation. A Fortran program implementing the same algorithm is given in [1].

Limitations

The function to be minimized must be continuous. fminbnd may only give local solutions.

fminbnd often exhibits slow convergence when the solution is on a boundary of the interval.

fminbnd only handles real variables.

See Also

fminsearch, fzero, optimset, function_handle (@), inline

References

Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.

fmin

fmins