MATLAB Function Reference

besselk

Modified Bessel function of the second kind

Syntax

• K = besselk(nu,Z)
  K = besselk(nu,Z,1)
  [K,ierr] = besselk(...)
  

Definitions

The differential equation

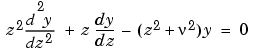
where 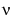is a real constant, is called the modified Bessel's equation, and its solutions are known as modified Bessel functions.

A solution 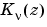of the second kind can be expressed as

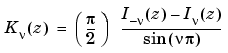
where 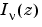and 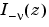form a fundamental set of solutions of the modified Bessel's equation for noninteger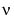

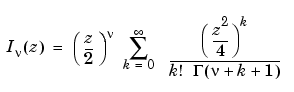
and 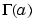is the gamma function. 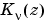is independent of .

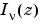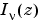can be computed using besseli.

Description

K = besselk(nu,Z) computes the modified Bessel function of the second kind, 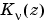, for each element of the array Z. The order nu need not be an integer, but must be real. The argument Z can be complex. The result is real where Z is positive.

If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, it is expanded to the other input's size. If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

K = besselk(nu,Z,1) computes besselk(nu,Z).*exp(Z).

[K,ierr] = besselk(...) also returns completion flags in an array the same size as K.

ierr	Description
0	besselk succesfully computed the modified Bessel function for this element.
1	Illegal arguments.
2	Overflow. Returns Inf.
3	Some loss of accuracy in argument reduction.
4	Unacceptable loss of accuracy, Z or nu too large.
5	No convergence. Returns NaN.

Examples

Example 1.

• format long
  z = (0:0.2:1)';
  
  besselk(1,z)
  
  ans =
                  Inf
     4.77597254322047
     2.18435442473269
     1.30283493976350
     0.86178163447218
     0.60190723019723
  

Example 2. besselk(3:9,(0:.2:10)',1) generates part of the table on page 424 of [1] Abramowitz and Stegun, Handbook of Mathematical Functions.

Algorithm

The besselk function uses a Fortran MEX-file to call a library developed by D. E. Amos [3] [4].

See Also

airy, besselh, besseli, besselj, bessely

References

[1]  Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sections 9.1.1, 9.1.89 and 9.12, formulas 9.1.10 and 9.2.5.

[2]  Carrier, Krook, and Pearson, Functions of a Complex Variable: Theory and Technique, Hod Books, 1983, section 5.5.

[3]  Amos, D. E., "A Subroutine Package for Bessel Functions of a Complex Argument and Nonnegative Order," Sandia National Laboratory Report, SAND85-1018, May, 1985.

[4]  Amos, D. E., "A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order," Trans. Math. Software, 1986.

besselj

bessely