Hexaflexagons


Old collection of hexaflexagons. All up to order 10 and some more.

Hexaflexagons are paper hexagons folded from strips of equilateral triangles, that show a number of different faces when folded by opening them at the center.

Here is a scanned copy of a "catalog" that I once compiled (~1973) of all possible hexaflexagons up to order 10.

The pictures show the forms of the strips and the several Tuckerman traverses (TT) that can be obtained from each strip, as diagrams of interconnected triangles that describe how the faces appear in the hexaflexagon. The numbers adjacent to most of the TTs indicate the folding sequence in the strip that produce them. The strip is to be folded at the triangle joints indicated by the numbers, starting from the arrow, or from the left, always in the same direction, with the sequence repeated 3 times at equally spaced points of the strip. When there is more than one line, the initial folding results in a straight strip, that is to be folded as the strip of the hexaflexagons of order 6 or 9, starting from the listed joints. Once obtained a strip with 9 triangles and a tab, it is folded as the trihexaflexagon.

Note that the number of possible hexaflexagons of order N is precisely the number of possible TTs, or the number of ways where N-2 triangles can be connected by their corners, with only two triangles per connection and without forming loops.

The background image shows the TTs of the 12 hexaflexagons of order 8

I wrote a program named HexaFind (rewriting an Algol program that I wrote by 1977) that finds all the possible TTs for given orders of hexaflexagons. In the present version it can also show the face numbers corresponding to the nodes, and, using the "reflectocloning" method developed by David King, show the strips that when folded result in hexaflexagons with those state diagrams. The program runs in Windows (2019). There is also an old DOS version (1999) here.
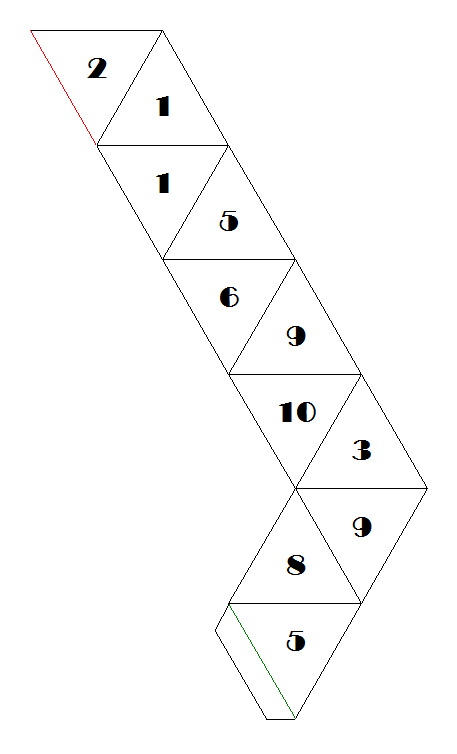
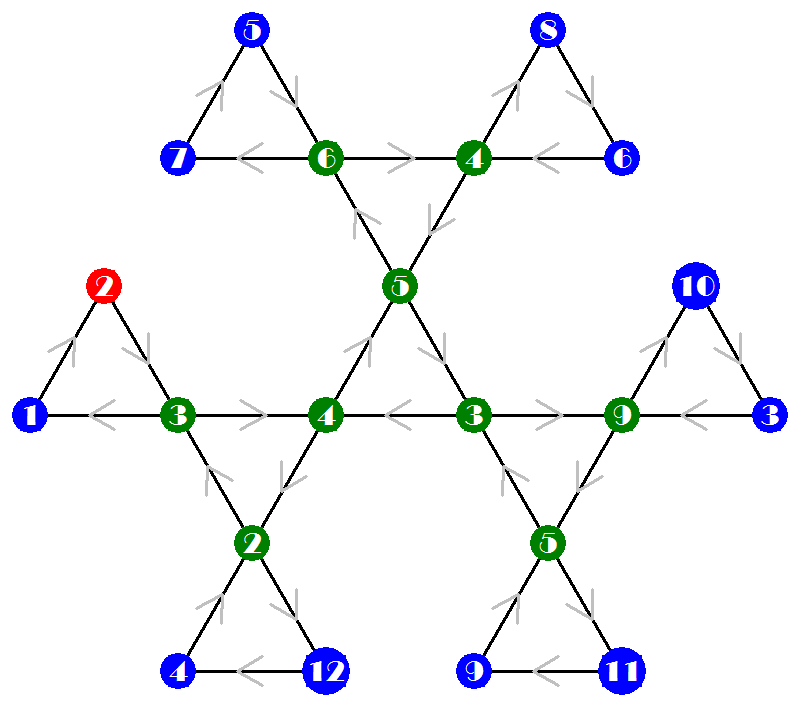
Example: The Tuckerman traverses of the last hexaflexagon of order 10 (#82), and the strip that produces it, front side and back side:

 
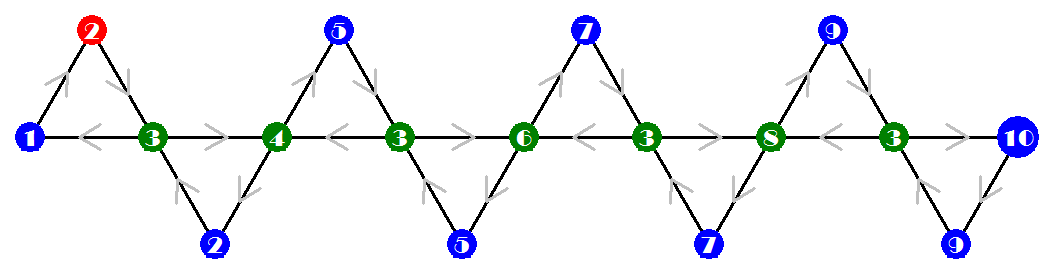
#82 of order 10.


 
Strip, front side and back side (with horizontal flip).

There are 82 possible hexaflexagons of order 10. This is the last one. The drawings of the strips generated by the program can be processed in any drawing program and printed. With some adjustment the images of the front and back sides, as the ones above, can be printed aligned at both sides of a paper sheet. The lines can be deleted from one side to simplify the alignment (the program can generate just the numbers too). In this example the strip is planar, but some have overlaps, complicating the printing and requiring some assembly. The program can also generate just 1/3 of the strip, to be replicated 3 times, what avoids overlaps in many cases, but not all. The parts can be joined with glued paper tabs, that may also be used to close the folded flexagon.  Avoid tape, as it will decay in little time. The assembly is done by first folding back and forth all the joints, and then folding together adjacent identical numbers, including pairs that appear in the folded strip. There are always three pairs of each. Paper clips (three) can be used to hold the folded strip during the folding. It's not easy to make hexaflexagons of  high order, greater than 12, because the faces accumulate in several positions (the blue faces) deforming the flexagon and making it difficult to fold. After the assembly, the outer sides of single sheet triangle faces (they appear in the blue corners in the map) can be trimmed with scissors, turning the folding easier.

Example: The last hexaflexagon of order 11, #228, and the 1/3 strip that generates it. In this way a larger flexagon, easier to fold, can be generated. The back face is represented by just the numbers, to simplify alignment with both images printed in both sides of a paper sheet. A tab was added to join the strips with glue. Three copies are needed, with the central copy mounted with the back side up. In the final flexagon, some faces appear with black numbers (1, 5, 9) others with red numbers (4, 7, 11) and some mixed (2, 3, 6, 8, 10).


#228 of order 11.

1/3 strip, to be replicated 3 times.

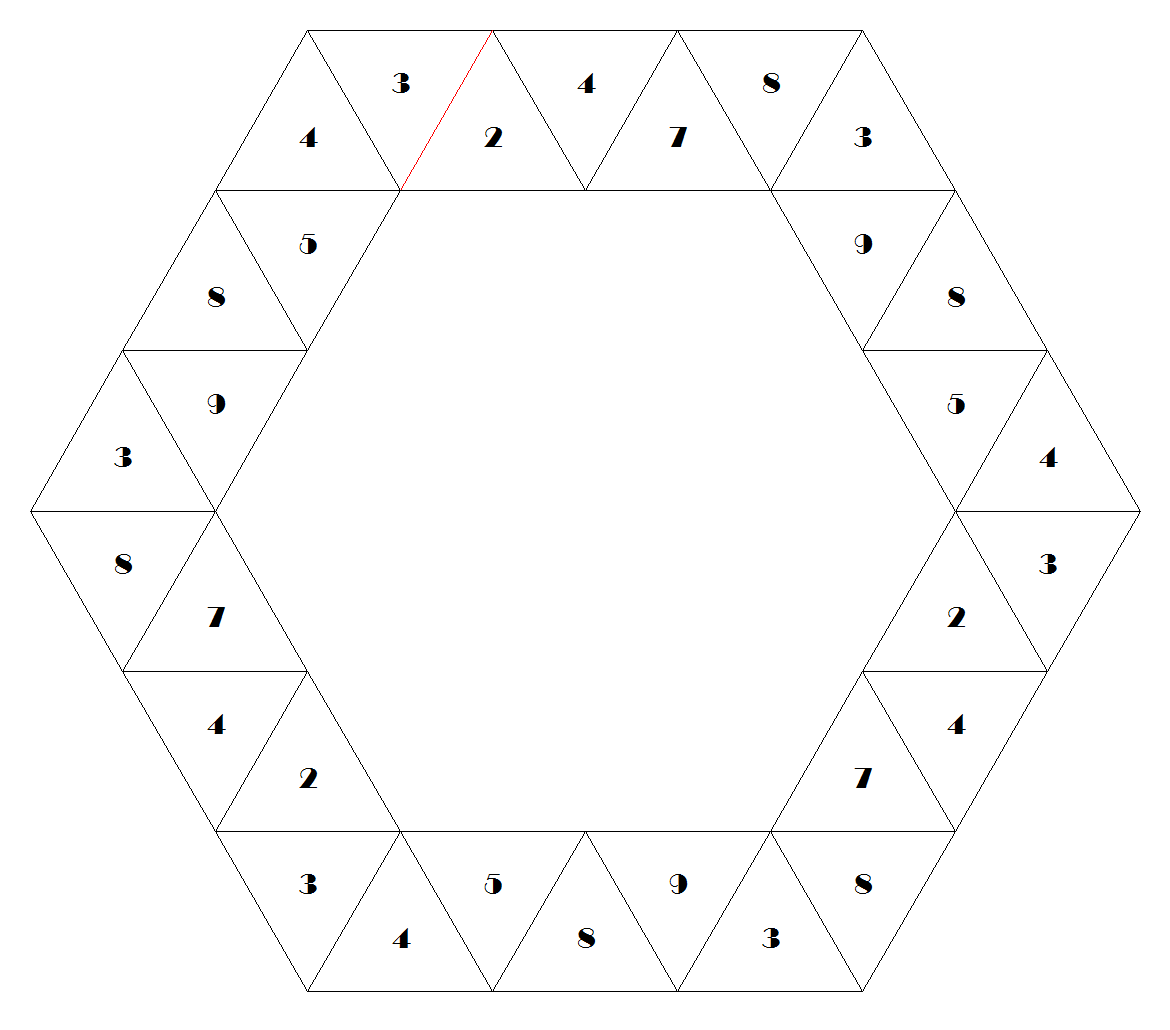
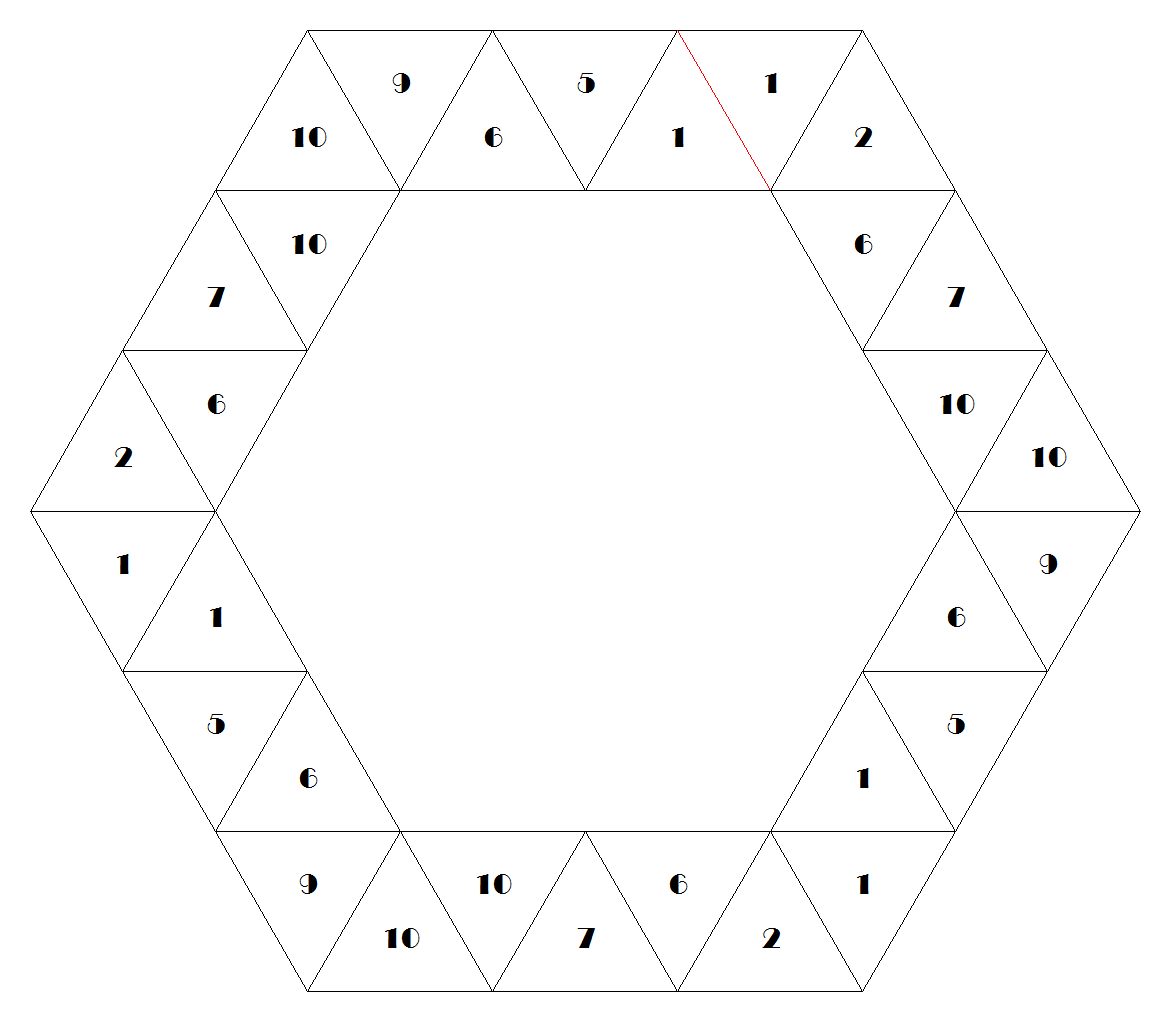
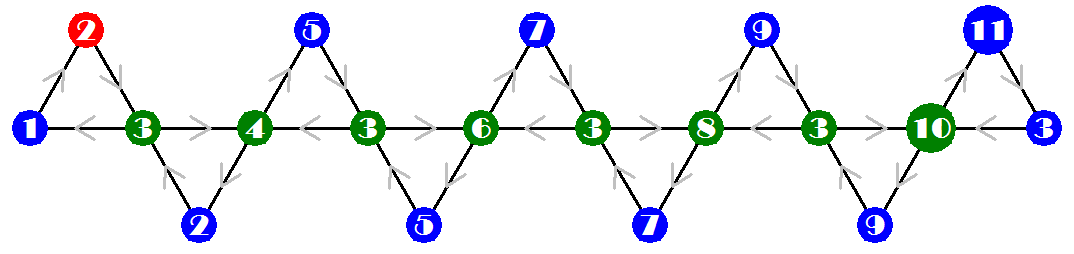
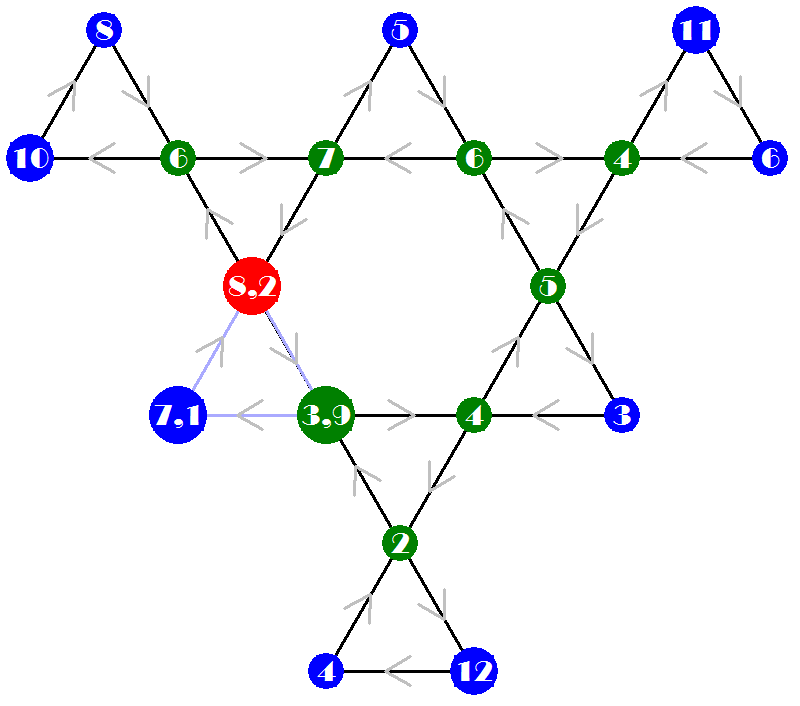
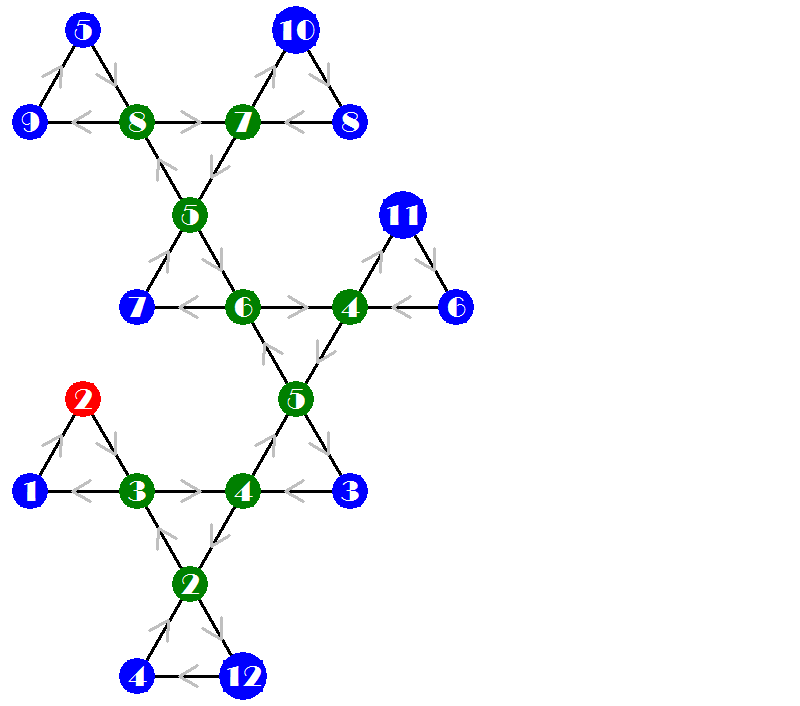
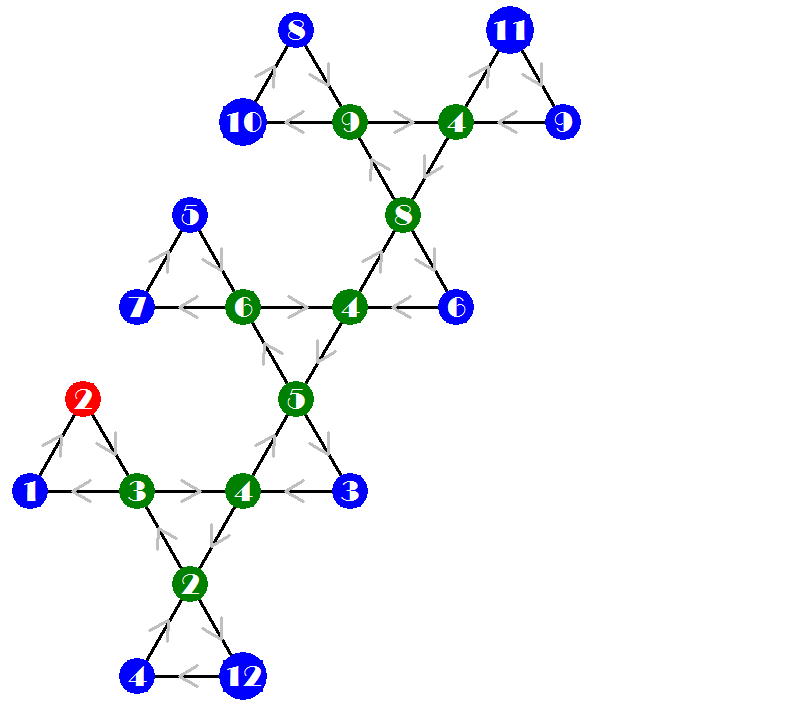
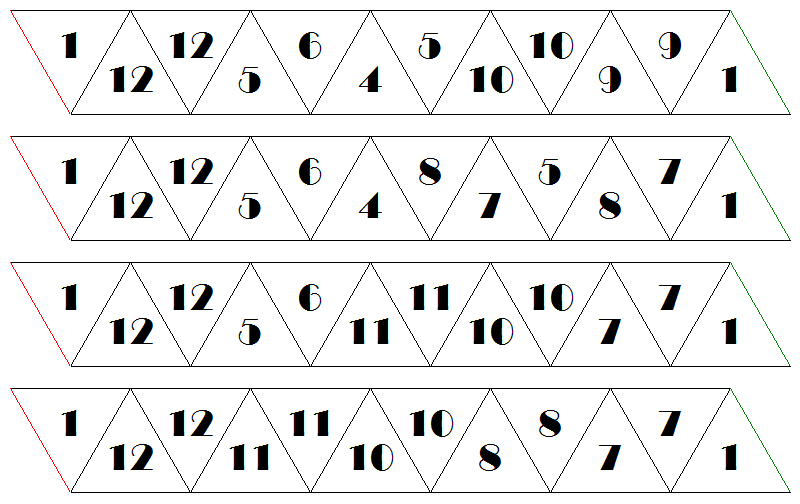
Example: The dodecahexaflexagon, with 12 faces, has 733 possibilities, and admits a straight strip with 36 triangles. This strip can be folded in 4 different ways, producing 4 different maps, shown below. A template for the four possibilities was assembled from the drawings made by the program. The two sides shall be printed well centered in both sides of the same sheet, in three copies to be joined without inversions. A portrait print requires no adjustment in most printers. A landscape printing, for larger size, requires centering in the longer direction of the sheet for correct alignment. The most well known version is #632, that is folded twice as an hexahexaflexagon. It is the only one of the four where the numbers in all the faces appear with the same color.


#92 and #412.

#595 and # 632.

Front faces, for the dodecahexaflexagons #92, #412, #595, and #632, 1/3 strips.


Back faces of the 1/3 strips, #92, #412, #595, and #632, (with horizontal flip).


All assembled and tested.

See my links about other subjects, including hexaflexagons

Established: 31/01/1999
Last update: 06/08/2019
Antonio Carlos M. de Queiroz
Lamento informar que o Prof. Antonio Carlos Moreirão de Queiroz faleceu há algum tempo.
Sei que esta página é visitada constantemente. Assim, gostaria de saber se temos algum visitante (interessado) que seja da UFRJ. Se for, por favor, envie um e-mail para watanabe@coe.ufrj.br.
Comento que é impressionante ver o que Moreirão foi capaz de fazer. Ele não só projetou os circuitos, mas também fez todo o trabalho de marceneiro (melhor que muitos que já vi e eram profissionais).
Segundo Moreirão contou em uma palestra, ele só levou choque uma vez. Sem querer encostou o dedo médio em um capacitor com alta tensão que se descarregou através do dedo. A corrente ao passar por uma das articulações a danificou e doía sempre que dobrava esse dedo. Mas, segundo ele, já tinha acostumado.
E. Watanabe (ELEPOT)