Signal Processing Toolbox

離散フーリエ変換

離散フーリエ変換(DFT)は、ディジタル信号処理の基本ツールです。Signal Processing Toolboxの基本は、高速フーリエ変換(FFT)で、高速にDFTを計算するものです。(z領域周波数応答、スペクトル解析、セプストラム解析、いくつかのフィルタ設計関数やフィルタ操作関数を含む)、多くのツールボックス関数には、FFTが組み込まれています。

MATLABには、離散フーリエ変換と逆フーリエ変換を計算する関数fftおよびifftが用意されています。入力列xとその変換列X(単位円周上の等間隔の周波数での離散系フーリエ変換)に対して、この2つの関数は、つぎの関係を実現します。

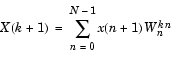
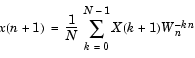
これらの方程式では、級数の添字は0ではなく1から始まります。それは、MATLABのベクトルインデックス方式によるものです。また、つぎの関係があります。

注意    MATLABは、関数fftに負の符号のjを使用しています。これは工学上の慣例であり、物理学や純粋数学では一般に正の符号のjを使用します。

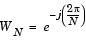
fftは、単一の入力引数xにより、入力ベクトルまたは行列のDFTを計算します。fftは、xがベクトルの場合ベクトルのDFTを計算します。また、xが長方形配列の場合、配列の各列のDFTを計算します。

たとえば、つぎの時間ベクトルと信号を作成します。

t = (0:1/99:1);                     % 時間ベクトル
x = sin(2*pi*15*t) + sin(2*pi*40*t);% 信号

信号のDFT、ならびに変換データ列のゲインと位相をつぎのように求めます。

y = fft(x);                       % xのDFTを計算
m = abs(y); p = unwrap(angle(y)); % ゲインと位相

このゲインと位相をプロットするには、つぎのようにします。

f = (0:length(y)-1)*99/length(y); % 周波数ベクトル
plot(f,m)
set(gca,'XTick',[15 40 60 85]);
plot(f,p*180/pi)
set(gca,'XTick',[15 40 60 85]);

fftの2番目の入力引数は、変換に用いる点数nを設定するものであり、DFTの長さを表します。

y = fft(x,n);

この場合、fft は、n よりも短い場合は、ゼロを付加し、n よりも長い場合は、打ち切ります。n が設定されていない場合、デフォルトとして、入力列の長さを使います。fft の実効時間は、処理する DFT の長さ n に依存します。このアルゴリズムに関する詳細については、MATLAB ドキュメント の fft リファレンスページを参照してください。

逆離散フーリエ変換関数ifftもまた入力列を受け取ります。また、オプションとして、変換に用いる点数も任意に設定できます。つぎの例題を試してください。オリジナルのデータ列xと再構成列は一致します(丸め誤差の範囲内で)。

t = (0:1/255:1);
x = sin(2*pi*120*t);
y = real(ifft(fft(x)));

このツールボックスは、2次元FFT用の関数であるfft2とその逆の関数であるifft2も含んでいます。これらの関数は、2次元の信号や画像の処理に役立ちます。詳細については、第6章のリファレンスを参照してください。

場合によっては、関数fftまたは関数fft2の出力を再配列してゼロ周波数成分が列の中央に来るようにすると便利なことがあります。MATLABの関数fftshiftは、ゼロ周波数成分をベクトルまたは行列の中央に移動します。

線形システム間の変換

参考文献