Signal Processing Toolbox

非因果的ゼロ位相フィルタの実現

FIRフィルタの場合、(filter、または、convを用いて)データに適用して、決まった数のサンプル数だけ単に出力を遅延させる線形位相フィルタを設計することができます。しかし、IIRフィルタの場合には、通常、位相歪みは強い非線形的なものになります。関数filtfiltは、現在の点の前後にある点(現在の点をもとに過去のデータと未来のデータ)の信号の情報を用いて位相歪みを除去します。すなわち、過去のデータのみでなく、"未来のデータ"を使って処理します。

filtfiltが、これを行う方法を理解するには、実数列x(n) のz変換をX(z)とすると、時間を反転した列x(n)のz変換は、X(1/z)となることを思い出してください。つぎの処理を考えます。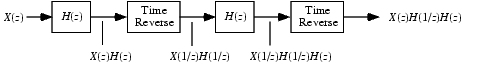

|z| = 1、すなわち、 z = e^jωのとき、出力はX(e^jω)|H(e^jω)|²になります。データ列x(n)のすべてのサンプルを与えると、位相歪みのないxの2回フィルタ処理を行なった結果を得ます。

たとえば、3 Hzと40 Hzの2つの正弦波成分からなる100 Hzでサンプリングした1秒間の信号は、

fs = 100;
t = 0:1/fs:1;
x = sin(2*pi*t*3)+.25*sin(2*pi*t*40);

つぎに、10点の平均化FIRフィルタを作成し、比較のために、filterとfiltfiltの両方を用いて、xをフィルタ処理します。

b = ones(1,10)/10;             % 10点平均フィルタ
y = filtfilt(b,1,x);           % 非因果的フィルタ処理
yy = filter(b,1,x);            % 通常のフィルタ処理
plot(t,x,t,y,'--',t,yy,':')

どちらのフィルタ処理形も、オリジナルの実線に見えている40  Hzの正弦波を除去しています。また、プロット図からは、filterとfiltfiltの違いも見ることができ、破線(filtfilt)はオリジナルの3 Hzの正弦波と同相ですが、点線(filter)は約5サンプル分遅れていることがわかります。また、破線の振幅はfiltfiltの大きさが2乗の効果により小さくなっています。

filtfiltは、初期条件を注意深く選択し、入力列の一部を加えることにより、フィルタ処理開始時の過渡状態を抑えます。最良の結果を得るには、フィルタ処理を行うデータ列が少なくともフィルタ次数の3倍以上の長さをもつようにし、データの両端でゼロを付加してください。

フィルタ処理のための関数

周波数領域フィルタの実現