

| MATLAB Function Reference |   |
表示
yi = pchip(x,y,xi) pp = pchip(x,y)
詳細
yi = pchip(x,y,xi)
は、ベクトル x と y で実行する区分的キュービック内挿を使って、xi の要素に対応して、計算された要素を含むベクトルyi を出力します。ベクトル x は、データ y が与えられる時点で、点を指定します。 y が行列の場合、内挿は、 y の各列に対して行われ、yi は、 length(xi) 行 size(y,2) 列になります。
pp = pchip(x,y)
は、 ppval による使用に対して、区分的な多項式構造を戻します。x は、行ベクトルでも、列ベクトルでも構いません。y は、x と同じ長さの行、または、列ベクトル、または、length(x) 列をもつ行列のいずれかです。
pchip は、中間点で、内挿する関数 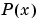 の値を求めます。
の値を求めます。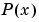 は、つぎの事柄を満足します。
は、つぎの事柄を満足します。
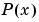 は、各サブ区間
は、各サブ区間 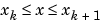 で、異なるキュービックです。
で、異なるキュービックです。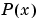 は、データを内挿します。すなわち、
は、データを内挿します。すなわち、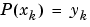 です。
です。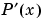 は、連続です。
は、連続です。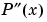 は、区分的線形です。
は、区分的線形です。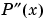 は、多分連続ではありません。すなわち、
は、多分連続ではありません。すなわち、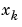 で、ジャンプする可能性があります。
で、ジャンプする可能性があります。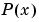 は、データの型と単調さを保存しています。
は、データの型と単調さを保存しています。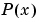 です。
です。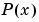 とします。
とします。spline は、スムーズです。すなわち、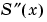 は連続です。
は連続です。spline は、データが平滑関数の値の場合、より正確になります。pchip は、データが平滑関数でない場合、オーバーシュートが生じず、振動が少なくなります。pchip は、設定が簡単です。例題
x = -3:3;
y = [-1 -1 -1 0 1 1 1];
t = -3:.01:3;
p = pchip(x,y,t);
s = spline(x,y,t);
plot(x,y,'o',t,p,'-',t,s,'-.')
legend({'data','pchip','spline'})
参考
参考文献
Fritsch, F. N. and R. E. Carlson, "Monotone Piecewise Cubic Interpolation," SIAM J. Numerical Analysis, Vol. 17, 1980, pp.238-246.
Kahaner, David, Cleve Moler, Stephen Nash, Numerical Methods and Software, Prentice Hall, 1988.
 | pcg | pcode |  |