nnls (MATLAB Function 参考文献)

非負の最小二乗法 Nonnegative least squares

注意： この関数の名前は、Release 11 (MATLAB 5.3) で、lsqnonneg に変更されたものです。関数 nnls は、Release 11 でサポートされていて、将来のバージョンでは削除される予定なので、関数 lsqnonneg と使ってください。

表示

x = nnls(A,b)
x = nnls(A,b,tol)
[x,w] = nnls(A,b)
[x,w] = nnls(A,b,tol)

詳細

x = nnls(A,b) は、方程式システム Ax = b を解ベクトルx が負の要素をもたないという条件 x_j > 0, j = 1, 2, ... n のもとで、最小2乗法的に解きます。解 x は、x 0 の基で、を最小化します。

x = nnls(A,b,tol) は、方程式システムを解き、許容値tol を指定します。デフォルトでは、tolは、max(size(A))*norm(A,1)*eps です。

[x,w] = nnls(A,b) は、対のベクトル w も出力します。ここで、x_i = 0 の場合、w_i 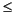0 で、x_i > 0 の場合、w_i 0 です。

[x,w] = nnls(A,b,tol) は、方程式システムを解き、対のベクトルw を出力し、許容値 tol を指定します。

例題

4 行 2 列の問題を、nnls 解法と制約のない最小2乗法とで比較します。

A =
    0.0372    0.2869
    0.6861    0.7071
    0.6233    0.6245
    0.6344    0.6170
b =
    0.8587
    0.1781
    0.0747
    0.8405
[A\b nnls(A,b)] =
    -2.5627         0
     3.1108   0.6929

[norm(A*(a\b)-b) norm(A*nnls(a,b)-b)] =
     0.6674 0.9118

nnls からの解はあまりよくありませんが、負の成分をもちません。

アルゴリズム

関数 nnls は、参考文献 [1] の23章に記述されているアルゴリズムを使用します。そのアルゴリズムは、取り得る1組の基本ベクトルの設定から出発し、それに関係した対のベクトルw を計算します。そして、w 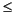0 になるまで基本ベクトルを変化させ、w の中の最大値に対応する基本ベクトルを求めます。

参考

\ 行列の左除算 (バックスラッシュ)

参考文献

[1] Lawson, C. L. and R. J. Hanson, Solving Least Squares Problems, Prentice-Hall, 1974, Chapter 23.

nextpow2 nnz