MATLAB Function Reference

erf, erfc, erfcx, erfinv

誤差関数

表示

Y = erf(X)                      誤差関数
Y = erfc(X)                     相補誤差関数
Y = erfcx(X)                    スケーリング相補誤差関数
X = erfinv(Y)                   逆誤差関数

定義

誤差関数 erf(X) は、平均値が0、分散が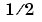のガウス分布の積分を2倍したものです。

相補誤差関数 erfc(X) は、つぎのように定義されます。

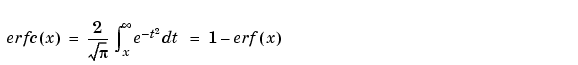
スケーリング相補誤差関数 erfcx(X) は、つぎのように定義されます。

大きな X に対して、erfcx(X) は、つぎの式で近似されます。

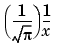
詳細

Y = erf(X) は、実数配列 X の各要素に対する誤差関数値を出力します。

Y = erfc(X) は、相補誤差関数の値を計算します。

Y = erfcx(X) は、スケーリング相補誤差関数の値を計算します。

X = erfinv(Y) は、Y の各要素に対して逆誤差関数の値を計算します。Y の要素は、範囲 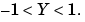内の値でなければなりません。

例題

erfinv(1) は、Infになります。

erfinv(-1) は、-Infになります。

abs(Y) > 1 に対して、 erfinv(Y) は、NaNになります。

注意

誤差関数と標準的な正規確率分布との間には、つぎような関係があります。

x = -5:0.1:5;
standard_normal_cdf = (1 + (erf(x/sqrt(2))))./2;

アルゴリズム

誤差関数に対するMATLAB のコードは、アルゴンヌ国立研究所の W. J. Cody によって書かれたFortranプログラム(NETLIB/SPECFUN, March 19, 1990)を変換したものです。主な計算は、参考文献[1]にある near-minimax有理数近似です。

逆誤差関数に対しては、重要な6桁までの正確な有理数近似が初期近似を生成するために使われます。これは、Newton法の2つのステップによって十分な精度に改良されています。 Newton法の改良版を削除するように、M-ファイルは簡単に修正できます。この結果、実行時間は 3倍速くなりますが、計算精度は悪くなります。

参考文献

[1] Cody, W. J., "Rational Chebyshev Approximations for the Error Function," Math. Comp., pgs. 631-638, 1969

eps

error