MATLAB Function Reference    
cholinc

スパース不完全コレスキ分解とコレスキ無限分解

表示

詳細

cholincは、2種類の不完全コレスキ分解を出力します。それらは、ドロップトレランスと、0レベルの要素が満たされている分解です。これらの分解は、pcg(前提条件付き共役傾斜法)のような繰り返し手法により解かれる対称正定行列システムの線形方程式に対する前提条件として、有効です。cholincは、スパース行列のみに対して機能します。

R = cholinc(X,droptol) は、ドロップトレランスdroptolを使って、Xの不完全コレスキ分解を行います。

R = cholinc(X,options) は、オプションを使って不完全コレスキ分解を行います。optionsは、最大3つのフィールドをもつ構造体です。

droptol
 不完全分解のドロップトレランスです。
michol
 修正不完全コレスキです。
rdiag
 Rの対角上のゼロを置き換えます。

注目するフィールドのみを設定できます。

droptolは、不完全コレスキ分解でドロップトレランスとして使用される、非負のスカラです。この分解は、不完全LU分解を使って計算されます。これは、ピボットしきい値のオプションを0に設定(対角要素を強制的にピボットさせます)し、列の対角要素の平方根によって、不完全上三角因子の行をスケーリングすることで計算されます。非ゼロ要素U(i,j)は、droptol*norm(X(:,j))よりも大きい(luincを参照)ので、非ゼロ要素R(i,j)は、droptol*norm(X(:,j))/R(i,i)よりも大きくなります。

と設定すると、デフォルトである不完全コレスキ分解を行います。

micholは、修正不完全コレスキ分解を意味します。この値は、0(修正なしコレスキ分解、デフォルト)または1(修正コレスキ分解)です。これは、Xの修正不完全LU分解を実行し、出力された上三角因子を上記のようにスケーリングします。

rdiagは、0または1です。1であれば、上三角因子Rの対角上のゼロは特異な要素を避けるために、ローカルなドロップトレランスの平方根で置き換えられます。デフォルトは、0です。

R = cholinc(X,'0') は、要素がレベル0で満たされている(すなわち充填されていない)実数対称正定スパース行列の不完全コレスキ分解を出力します。キャンセルのためにXが非ゼロである位置で、Rがゼロであっても、上三角行列Rは、triu(X)と同じスパースパターンです。Xの下三角行列は、上三角行列の転置と仮定されます。Xの正定性は、要求されているスパース性をもつ因子の存在を保証しないことに注意してください。分解できなければ、エラーメッセージが表示されます。分解がうまくいくと、R'*Rは、スパースパターンにおいてXと一致します。

[R,p] = cholinc(X,'0') は、2つの出力引数をもち、エラーメッセージを表示しません。Rが存在すれば、pは0です。しかし、不完全因子が存在しなければ、pは正の整数で、Rは、q = p-1のとき、q行n列の上三角行列で、Rのスパースパターンは、Xのq行n列の上三角行列のスパースパターンになります。R'*Rは、最初のq行とq列のスパースパターンが、Xと一致します。

R = cholinc(X,'inf') は、コレスキ無限分解を行います。この分解は、コレスキ分解に基づいており、さらに実数の準正定行列を扱います。内点法で生じるシステムの解を見つけるために有効です。ゼロピボットが通常のコレスキ分解で生じるとき、コレスキ無限因子の対角がInfに設定され、その行の残りは0に設定されます。これは、線形方程式に関連するシステム内の解ベクトルの対応するエントリを強制的に0にします。実際に、負のピポッドが、Infで、置き換えられたときでさえ、Xは、準正定行列と仮定されています。

注意

これらの不完全分解は、大きなスパースシステム線形方程式を解くための前提条件として有効です。上三角因子の対角上に1つの0があると、行列は特異になります。ドロップトレランスをもつ不完全分解は、上三角因子の対角上に0がある場合、ワーニングメッセージを表示します。同様に、ゼロ対角を置き換えるためにrdiagオプションを使うと、問題の徴候がなくなるだけで、解くことはしません。前提条件は特異でない場合もありますが、有効ではなく、ワーニングメッセージが表示されます。

コレスキ無限分解は、内点法でのみ使用することを意図しています。それ以外での使用は推奨しません。

例題

例題 1.

対称正定行列Sから始めます。

Sは、numgrid('C',15)で作成されるグリッド上の2次元負の5点離散Laplacianです。

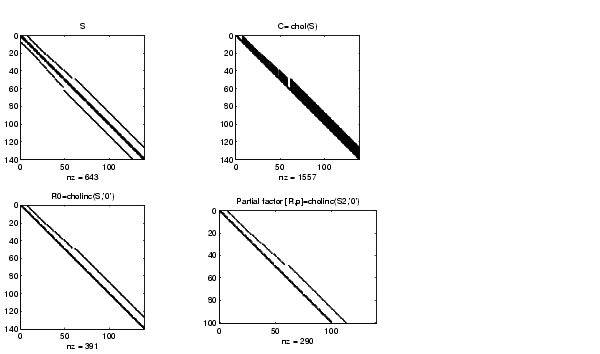
要素の充填の比較のために、コレスキ分解とレベル0のコレスキ分解を計算します。対角要素をゼロにすることでSを特異にし、レベル0の(部分的)不完全コレスキ分解を計算します。

完全コレスキ分解では、Sの対角帯は要素が満たされていますが、不完全コレスキ分解では満たされていません。特異行列S2の不完全分解は、p = 101行で停止し、結果として100行139列の部分的な分解となります。

D1はeps程度の要素をもち、R0'*R0とSのスパースパターンが一致することを示します。D2は、最初の100行と100列、D2(1:100,:)とD2(:,1:100)にeps程度の要素をもちます。

例題 2.

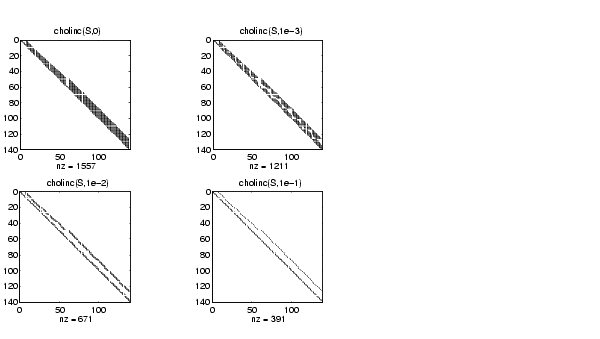
下図の最初のサブプロットは、ドロップトレランス0での不完全コレスキ分解cholinc(S,0)が、Sのコレスキ分解と同じであることを示します。ドロップトレランスが大きくなると、下図のように不完全分解のスパース性が増加します。

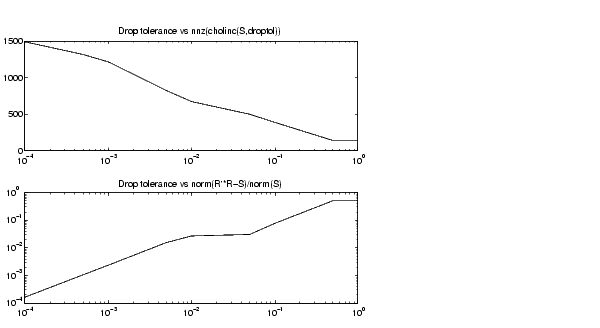
残念なことに、つぎの図のドロップトレランスとnorm(R'*R-S,1)/norm(S,1)のプロットに見られるように、スパースな分解の近似は良くありません。

例題 3

ヒルベルト行列は、(i,j)要素が 1/(i+j-1)で表わされる行列で、理論的に正定行列です。

特に、コレスキ因子分解は、より大きな行列を小さいものに分解します。

このhilb(20)に対して、 コレスキ分解は、14行目で数値的にゼロのピポットのために計算が失敗に終わります。このエラーを避けるために、コレスキ無限因子分解を使います。ゼロピポットに出会うと、cholincは、主対角行列にInfを設定します。そして、行の残りにゼロを設定し、計算を続けます。

この場合、14行以降のピポットはすべて小さくて、上三角分解の残りは、つぎのようになります。

制限

cholincは、正方スパース行列のみに動作します。cholinc(X,'0')とcholinc(X,'inf')については、Xは実数でなければなりません。

アルゴリズム

R = cholinc(X,droptol)は、[L,U] = luinc(X,options)から得られます。ここで、options.droptol = droptolで、options.thresh = 0です。上三角行列Uの行は、その行の対角要素の平方根でスケーリングされ、スケールファクタはRになります。

R = cholinc(X,options) は、rdiagオプションがudiagオプションに変わり、miluオプションがmicholオプションの値をとることを除けば、同様の方法で作られます。

R = cholinc(X,'0') は、コレスキ分解の変形である"KJI"を基本にしています。Xの上三角部分の非ゼロ要素の位置に対してのみランク1の行列を加えます。

R = cholinc(X,'inf') は、Zhangのアルゴリズムに基づいています。

参考

chol, luinc, pcg

参考文献

[1] Saad, Yousef, Iterative Methods for Sparse Linear Systems, PWS Publishing Company, 1996, Chapter 10 - Preconditioning Techniques.

[2] Zhang, Yin, Solving Large-Scale Linear Programs by Interior-Point Methods Under the MATLAB Environment, Department of Mathematics and Statistics, University of Maryland Baltimore County, Technical Report TR96-01


 chol cholupdate