Mathematics

特異値分解

長方形行列Aの特異値と対応する特異ベクトルは、つぎの式を満足するスカラ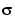とu,vの一組のベクトルで表されます。

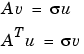
対角行列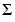の対角要素で表す特異値と、それに対応し、2つの直交行列の列からなる特異ベクトルUとVは、つぎの関係があります。

UとVは、直交なので、これは特異値分解になります。

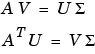
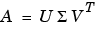
m行n列の行列のフル特異値分解は、m行m列のUとm行n列の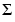とn行n列のVになります。言い換えれば、UとVは共に正方で、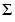はAと同じサイズです。Aが列数より行数のほうが多いと、結果求まるUは非常に大きくなり、その列の大部分は、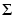の中のゼロと乗算されるものになります。このような場合、エコノミサイズの分解は、m行n列のUとn行n列の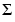と同じ大きさのVを作成し、時間的にもスペース的にもセーブされます。

固有値分解は、あるベクトル空間からそれ自身への射影を表すとき、すなわち、常微分方程式に対して行うとき、行列を解析するために適切なツールです。一方、特異値分解は、一つのベクトル空間を他のベクトル空間への射影を解析する適切なツールです。これは、異なる次元についても取り扱えます。ほとんどの連立方程式システムは、この2番目のカテゴリに入ります。

Aが正方で、対称、正定ならば、この固有値と特異値は等しくなります。しかし、Aが対称、正定でなくなると、2つの分解の結果のズレは大きくなります。特に、実数行列の特異値分解は、常に実数ですが、実数で非対称行列の特異値は複素数になることもあります。

例題の行列に対して、

A =
     9     4
     6     8
     2     7

フル特異値分解は、つぎのようになります。

[U,S,V] = svd(A)

U =
    0.6105   -0.7174    0.3355
    0.6646    0.2336   -0.7098
    0.4308    0.6563    0.6194

S =
   14.9359         0
         0    5.1883
         0         0

V =
    0.6925   -0.7214
    0.7214    0.6925

U*S*V'が、丸め誤差の範囲内でAに等しいことを確かめましょう。この小さな行列での問題に対しては、経済的な大きさでの分解が、わずかですが小さくなります。

[U,S,V] = svd(A,0)

U =
    0.6105   -0.7174
    0.6646    0.2336
    0.4308    0.6563

S =
   14.9359         0
         0    5.1883

V =
    0.6925   -0.7214
    0.7214    0.6925

U*S*V' は、丸め誤差の範囲内で Aに等しいことを確かめてください。

固有値

多項式と内挿