Using the C62x DSP Library (Embedded Target for Texas Instruments C6000 DSPs)

Embedded Target for Texas Instruments C6000 DSPs

Q Format Notation

The position of the binary point in a fixed-point number determines how you interpret the scaling of the number. When it performs basic arithmetic such as addition or subtraction, hardware uses the same logic circuits regardless of the value of the scale factor. In essence, the logic circuits have no knowledge of a binary point. They perform signed or unsigned integer arithmetic--as if the binary point is to the right of b₀. Therefore, you, the programmer, determine the binary point.

In the the C62x DSP Library, the position of the binary point in the signed, fixed-point data types is expressed in and designated by Q format notation. This fixed-point notation takes the form

Qm.n

where

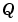designates that the number is in Q format notation--the Texas Instruments representation for signed fixed-point numbers.
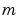is the number of bits used to designate the two's complement integer portion of the number.
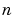is the number of bits used to designate the two's complement fractional portion of the number, or the number of bits to the right of the binary point.

In Q format, the most significant bit is always designated as the sign bit. Representing a signed fixed-point data type in Q format always requires m+n+1 bits to account for the sign.

Example--Q.15

For example, a signed 16-bit number with n = 15 bits to the right of the binary point is expressed as

```
Q0.15
```

in this notation. This is (1 sign bit) + (m = 0 integer bits) + (n = 15 fractional bits) = 16 bits total in the data type. In Q format notation the m = 0 is often implied, as in

```
Q.15
```

In the Fixed-Point Blockset, this data type is expressed as

```
sfrac16
```

```
sfix16_En15
```

In the Filter Design Toolbox, this data type is expressed as

```
[16 15]
```

Example--Q1.30

Multiplying two Q.15 numbers yields a product that is a signed 32-bit data type with n = 30 bits to the right of the binary point. One bit is the designated sign bit, thereby forcing m to be 1:

m+n+1 = 1+30+1 = 32 bits total

Therefore this number is expressed as

```
Q1.30
```

In the Fixed-Point Blockset, this data type is expressed as

```
sfix32_En30
```

In the Filter Design Toolbox, this data type is expressed as

```
[32 30]
```

Example--Q-2.17

Consider a signed 16-bit number with a scaling of 2^(-17). This requires n = 17 bits to the right of the binary point, meaning that the most significant bit is a sign-extended bit.

Sign extension fills additional bits with the value of the MSB. For example, consider a 4-bit two's complement number 1011. When this number is extended to 7 bits with sign extension, the number becomes 1111101 and the value of the number remains the same.

One bit is the designated sign bit, forcing m to be -2:

Therefore this number is expressed as

```
Q-2.17
```

In the Fixed-Point Blockset, this data type is expressed as

```
sfix16_En17
```

In the Filter Design Toolbox, this data type is expressed as

```
[16 17]
```

Example--Q17.-2

Consider a signed 16-bit number with a scaling of 2^(2) or 4. This means that the binary point is implied to be 2 bits to the right of the 16 bits, or that there are n = -2 bits to the right of the binary point. One bit must be the sign bit, thereby forcing m to be 17:

Therefore this number is expressed as

```
Q17.-2
```

In the Fixed-Point Blockset, this data type is expressed as

```
sfix16_E2
```

In the Filter Design Toolbox, this data type is expressed as

```
[16 -2]
```

Signed Fixed-Point Numbers Building Models