Symbolic Math Toolbox

Procedure Example

The following example shows how you can access a Maple procedure through the Extended Symbolic Math Toolbox. The example computes either symbolic or variable-precision numeric approximations to 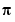, using a method derived by Richard Brent based from the arithmetic-geometric mean algorithm of Gauss. Here is the Maple source code:

• pie := proc(n)
    # pie(n) takes n steps of an arithmetic-geometric mean
    # algorithm for computing pi. The result is a symbolic
    # expression whose length roughly doubles with each step.
    # The number of correct digits in the evaluated string also
    # roughly doubles with each step.
  
    # Example: pie(5) is a symbolic expression with 1167
    # characters which, when evaluated, agrees with pi to 84
    # decimal digits.
  
    local a,b,c,d,k,t;
  
    a := 1:
    b := sqrt(1/2):
    c := 1/4:
    t := 1:
  
    for k from 1 to n do
       d := (b-a)/2:
       b := sqrt(a*b):
       a := a+d:
       c := c-t*d^2:
       t := 2*t:
    od;
  
    (a+b)^2/(4*c):
  
  end;
  

Assume the source code for this Maple procedure is stored in the file pie.src. Using the Extended Symbolic Math Toolbox, the MATLAB statement

• procread('pie.src')
  

reads the specified file, deletes comments and newline characters, and sends the resulting string to Maple. (The MATLAB ans variable then contains a string representation of the pie.src file.)

You can use the pie function, using the maple function. The statement

• p = maple('pie',5)
  

returns a string representing the solution that begins and ends with

• p = 
  1/4*(1/32+1/64*2^(1/2)+1/32*2^(3/4)+ ...
       ... *2^(1/2))*2^(3/4))^(1/2))^(1/2))^2)
  

You can use the SYM command to convert the string to a symbolic object. It is interesting to change the computation from symbolic to numeric. The assignment to the variable b in the second executable line is key. If the assignment statement is simply

• b := sqrt(1/2)
  

the entire computation is done symbolically. But if the assignment statement is modified to include decimal points

• b := sqrt(1./2.)
  

the entire computation uses variable-precision arithmetic at the current setting of digits. If this change is made, then

• digits(100)
  procread('pie.src')
  p = maple('pie',5)
  

produces a 100-digit result:

• p =
  3.14159265358979323 ... 5628703211672038
  

The last 16 digits differ from those of 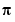because, with five iterations, the algorithm gives only 84 digits.

Note that you can define your own MATLAB M-file that accesses a Maple procedure:

• function p = pie1(n)
  p = maple('pie',n)
  

Packages of Library Functions

Precompiled Maple Procedures