Symbolic Math Toolbox

Diffraction

This example is from diffraction theory in classical electrodynamics. (J.D. Jackson, Classical Electrodynamics, John Wiley & Sons, 1962.)

Suppose we have a plane wave of intensity I₀ and wave number k. We assume that the plane wave is parallel to the xy-plane and travels along the z-axis as shown below. This plane wave is called the incident wave. A perfectly conducting flat diffraction screen occupies half of the xy-plane, that is x < 0. The plane wave strikes the diffraction screen, and we observe the diffracted wave from the line whose coordinates are (x, 0, z₀), where z₀ > 0.

The intensity of the diffracted wave is given by

where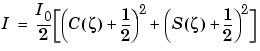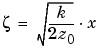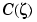

and and 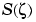are the Fresnel cosine and sine integrals:

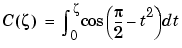
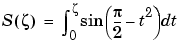
How does the intensity of the diffracted wave behave along the line of observation? Since k and z₀ are constants independent of x, we set

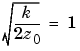
and assume an initial intensity of I₀ = 1 for simplicity.

The following code generates a plot of intensity as a function of x:

• x = -50:50;
  C = mfun('FresnelC',x);
  S = mfun('FresnelS',x);
  I0 = 1;
  T = (C+1/2).^2 + (S+1/2).^2;
  I = (I0/2)*T;
  plot(x,I);
  xlabel('x');
  ylabel('I(x)');
  title('Intensity of Diffracted Wave');
  

We see from the graph that the diffraction effect is most prominent near the edge of the diffraction screen (x = 0), as we expect.

Note that values of x that are large and positive correspond to observation points far away from the screen. Here, we would expect the screen to have no effect on the incident wave. That is, the intensity of the diffracted wave should be the same as that of the incident wave. Similarly, x values that are large and negative correspond to observation points under the screen that are far away from the screen edge. Here, we would expect the diffracted wave to have zero intensity. These results can be verified by setting

• x = [Inf -Inf] 
  

in the code to calculate I.

Special Mathematical Functions

Using Maple Functions