Using the Symbolic Math Toolbox (Symbolic Math Toolbox)

Symbolic Math Toolbox

Eigenvalues

The symbolic eigenvalues of a square matrix A or the symbolic eigenvalues and eigenvectors of A are computed, respectively, using the commands

```
E = eig(A)
[V,E] = eig(A)
```

The variable-precision counterparts are

```
E = eig(vpa(A))
[V,E] = eig(vpa(A))
```

The eigenvalues of A are the zeros of the characteristic polynomial of A, det(A-x*I), which is computed by

```
poly(A)
```

The matrix H from the last section provides our first example:

H =
[8/9, 1/2, 1/3]
[1/2, 1/3, 1/4]
[1/3, 1/4, 1/5]

The matrix is singular, so one of its eigenvalues must be zero. The statement

```
[T,E] = eig(H)
```

produces the matrices T and E. The columns of T are the eigenvectors of H:

T =
 
[    1, 28/153+2/153*12589^(1/2),  28/153-2/153*12589^(12)]
[   -4,                        1,                        1]
[ 10/3, 92/255-1/255*12589^(1/2), 292/255+1/255*12589^(12)]

Similarly, the diagonal elements of E are the eigenvalues of H:

E =
 
[0,                       0,                       0]
[0, 32/45+1/180*12589^(1/2),                       0]
[0,                       0, 32/45-1/180*12589^(1/2)]

It may be easier to understand the structure of the matrices of eigenvectors, T, and eigenvalues, E, if we convert T and E to decimal notation. We proceed as follows. The commands

```
Td = double(T)
Ed = double(E)
```

return

Td =
    1.0000    1.6497   -1.2837
   -4.0000    1.0000    1.0000
    3.3333    0.7051    1.5851
Ed =
    0         0         0
    0    1.3344         0
    0         0    0.0878

The first eigenvalue is zero. The corresponding eigenvector (the first column of Td) is the same as the basis for the null space found in the last section. The other two eigenvalues are the result of applying the quadratic formula to

```
x^2-64/45*x+253/2160
```

which is the quadratic factor in factor(poly(H)).

syms x
g = simple(factor(poly(H))/x);
solve(g)

Closed form symbolic expressions for the eigenvalues are possible only when the characteristic polynomial can be expressed as a product of rational polynomials of degree four or less. The Rosser matrix is a classic numerical analysis test matrix that happens to illustrate this requirement. The statement

```
R = sym(gallery('rosser'))
```

generates

 R = 
[ 611   196  -192   407    -8   -52   -49    29]
[ 196   899   113  -192   -71   -43    -8   -44]
[-192   113   899   196    61    49     8    52]
[ 407  -192   196   611     8    44    59   -23]
[  -8   -71    61     8   411  -599   208   208]
[ -52   -43    49    44  -599   411   208   208]
[ -49    -8     8    59   208   208    99  -911]
[  29   -44    52   -23   208   208  -911    99]

The commands

```
p = poly(R);
pretty(factor(p))
```

produce

                2                  2                      2
 x (x - 1020) (x  - 1020 x + 100)(x  - 1040500) (x - 1000)

The characteristic polynomial (of degree 8) factors nicely into the product of two linear terms and three quadratic terms. We can see immediately that four of the eigenvalues are 0, 1020, and a double root at 1000. The other four roots are obtained from the remaining quadratics. Use

```
eig(R)
```

to find all these values

[               0]
[            1020]
[510+100*26^(1/2)]
[510-100*26^(1/2)]
[  10*10405^(1/2)]
[ -10*10405^(1/2)]
[            1000]
[            1000]

The Rosser matrix is not a typical example; it is rare for a full 8-by-8 matrix to have a characteristic polynomial that factors into such simple form. If we change the two "corner" elements of R from 29 to 30 with the commands

```
S = R;  S(1,8) = 30;  S(8,1) = 30;
```

and then try

```
p = poly(S)
```

we find

p =
40250968213600000+51264008540948000*x-
   1082699388411166000*x^2+4287832912719760*x^-3-
   5327831918568*x^4+82706090*x^5+5079941*x^6-
   4040*x^7+x^8

We also find that factor(p) is p itself. That is, the characteristic polynomial cannot be factored over the rationals.

For this modified Rosser matrix

```
F = eig(S)
```

returns

F =
[ -1020.0532142558915165931894252600]
[ -.17053529728768998575200874607757]
[  .21803980548301606860857564424981]
[  999.94691786044276755320289228602]
[  1000.1206982933841335712817075454]
[  1019.5243552632016358324933278291]
[  1019.9935501291629257348091808173]
[  1020.4201882015047278185457498840]

Notice that these values are close to the eigenvalues of the original Rosser matrix. Further, the numerical values of F are a result of Maple's floating-point arithmetic. Consequently, different settings of digits do not alter the number of digits to the right of the decimal place.

It is also possible to try to compute eigenvalues of symbolic matrices, but closed form solutions are rare. The Givens transformation is generated as the matrix exponential of the elementary matrix

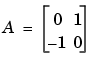
The Symbolic Math Toolbox commands

syms t
A = sym([0 1; -1 0]);
G = expm(t*A)

return

[  cos(t),  sin(t)]
[ -sin(t),  cos(t)]

Next, the command

```
g = eig(G)
```

produces

g =
[ cos(t)+(cos(t)^2-1)^(1/2)]
[ cos(t)-(cos(t)^2-1)^(1/2)]

We can use simple to simplify this form of g. Indeed, a repeated application of simple

for  j = 1:4
   [g,how] = simple(g)
end

produces the best result:

g =
[ cos(t)+(-sin(t)^2)^(1/2)]
[ cos(t)-(-sin(t)^2)^(1/2)]

how =
simplify

g =
[ cos(t)+i*sin(t)]
[ cos(t)-i*sin(t)]
 
how =
radsimp
 
g =
[   exp(i*t)]
[ 1/exp(i*t)]

how =
convert(exp)

g =
[  exp(i*t)]
[ exp(-i*t)]
 
how =
combine

Notice the first application of simple uses simplify to produce a sum of sines and cosines. Next, simple invokes radsimp to produce cos(t) + i*sin(t) for the first eigenvector. The third application of simple uses convert(exp) to change the sines and cosines to complex exponentials. The last application of simple uses simplify to obtain the final form.

Linear Algebraic Operations Jordan Canonical Form