| Spline Toolbox | |
What Is a Chebyshev Spline?
The Chebyshev spline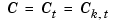 
of order 
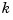for the knot sequence 
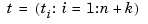is the unique element of 
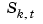of max-norm 1 that maximally oscillates on the interval 
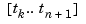and is positive near 
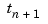. This means that there is a unique strictly increasing 
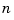-sequence 
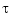so that the function 
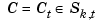given by 
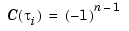, all 
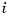, has max-norm 1 on 
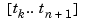. This implies that 
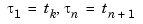, and that 
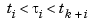, all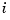 
. In fact, 
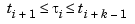, all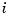 
. This brings up the point that the knot sequence is assumed to make such an inequality possible, i.e., the elements of 
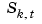are assumed to be continuous.
In short, the Chebyshev spline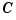 
looks just like the Chebyshev polynomial. It performs similar functions. For example, its extreme sites 
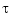are particularly good sites to interpolate at from 
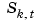since the norm of the resulting projector is about as small as can be; see the toolbox command chbpnt.
In this example, which can be run via chebdem, we try to construct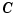 
for a particular knot sequence 
.
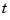| | Example: Construction of the Chebyshev Spline | Choice of Spline Space | |