Spline Toolbox

B-form

The B-form of this spline comprises the cell array 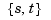of its knot sequences, the coefficient array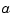 , the numbers vector 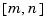, and the orders vector . The command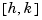

• sp = spmak();
  

constructs this form. Further, fnplt, fnval, fnder, fndir, fnrfn, and fn2fm can be used to plot, evaluate, differentiate and integrate, refine, and convert this form.

You are most likely to construct such a form by looking for an interpolant or approximant to gridded data. For example, if you know the values

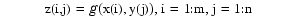
, of some function at all the points in a rectangular grid, then, assuming that the strictly increasing sequence x satisfies the Schoenberg-Whitney conditions with respect to the above knot sequence 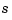, and that the strictly increasing sequence y satisfies the Schoenberg-Whitney conditions with respect to the above knot sequence 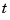, the command

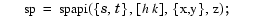
constructs the unique bivariate spline of the above form that matches the given values. The command fnplt(sp) gives you a quick plot of this interpolant. The command pp = fn2fm(sp,'pp') gives you the ppform of this spline, which is probably what you want when you want to evaluate the spline at a fine grid ((xx(i),yy(j)) for i=1:M, j=1:N), by the command:

• values = fnval(pp,{xx,yy});
  

Tensor Product Splines

ppform