| Spline Toolbox | |
Polynomials vs. Splines
Polynomials are the approximating functions of choice when a smooth function is to be approximated locally. For example, the truncated Taylor series
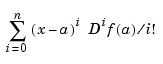
provides a satisfactory approximation for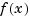 
if 
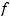is sufficiently smooth and 
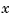is sufficiently close to 
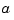. But if a function is to be approximated on a larger interval, the degree, 
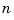, of the approximating polynomial may have to be chosen unacceptably large. The alternative is to subdivide the interval 
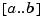of approximation into sufficiently small intervals 
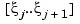, with
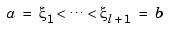, so that, on each such interval, a polynomial 
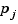of relatively low degree can provide a good approximation to 
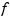. This can even be done in such a way that the polynomial pieces blend smoothly, i.e., so that the resulting patched or composite function 
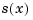that equals 
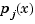for 
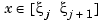, all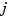 
, has several continuous derivatives. Any such smooth piecewise polynomial function is called a spline. I.J. Schoenberg coined this term since a twice continuously differentiable cubic spline with sufficiently small first derivative approximates the shape of a draftsman's spline.
There are two commonly used ways to represent a polynomial spline, the ppform and the B-form. In this toolbox, a spline in ppform is often referred to as a piecewise polynomial, while a piecewise polynomial in B-form is often referred to as a spline. This reflects the fact that piecewise polynomials and (polynomial) splines are just two different views of the same thing.
| | Splines: An Overview | ppform | |