Signal Processing Toolbox

stmcb

Compute a linear model using Steiglitz-McBride iteration

Syntax

• [b,a] = stmcb(h,nb,na)
  [b,a] = stmcb(y,x,nb,na)
  [b,a] = stmcb(h,nb,na,niter)
  [b,a] = stmcb(y,x,nb,na,niter)
  [b,a] = stmcb(h,nb,na,niter,ai)
  [b,a] = stmcb(y,x,nb,na,niter,ai)
  

Description

Steiglitz-McBride iteration is an algorithm for finding an IIR filter with a prescribed time domain impulse response. It has applications in both filter design and system identification (parametric modeling).

[b,a] = stmcb(h,nb,na) finds the coefficients b and a of the system b(z)/a(z) with approximate impulse response h, exactly nb zeros, and exactly na poles.

[b,a] = stmcb(y,x,nb,na) finds the system coefficients b and a of the system that, given x as input, has y as output. x and y must be the same length.

[b,a] = stmcb(h,nb,na,niter) and

[b,a] = stmcb(y,x,nb,na,niter) use niter iterations. The default for niter is 5.

[b,a] = stmcb(h,nb,na,niter,ai) and

[b,a] = stmcb(y,x,nb,na,niter,ai) use the vector ai as the initial estimate of the denominator coefficients. If ai is not specified, stmcb uses the output argument from [b,ai] = prony(h,0,na) as the vector ai.

stmcb returns the IIR filter coefficients in length nb+1 and na+1 row vectors b and a. The filter coefficients are ordered in descending powers of z.

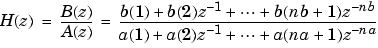
Examples

Approximate the impulse response of a Butterworth filter with a system of lower order:

• [b,a] = butter(6,0.2);
  h = filter(b,a,[1 zeros(1,100)]);
  freqz(b,a,128)
  
  
  [bb,aa] = stmcb(h,4,4);
  freqz(bb,aa,128)
  
  
  

Algorithm

stmcb attempts to minimize the squared error between the impulse response h of b(z)/a(z) and the input signal x.

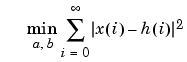
stmcb iterates using two steps:

1. It prefilters h and x using 1/a(z).
2. It solves a system of linear equations for b and a using \.

stmcb repeats this process niter times. No checking is done to see if the b and a coefficients have converged in fewer than niter iterations.

Diagnostics

If x and y have different lengths, stmcb produces this error message,

• Input signal X and output signal Y must have the same length.
  

See Also

levinson, lpc, aryule, prony

References

[1] Steiglitz, K., and L.E. McBride, "A Technique for the Identification of Linear Systems," IEEE Trans. Automatic Control, Vol. AC-10 (1965), pp. 461-464.

[2] Ljung, L., System Identification: Theory for the User, Prentice-Hall, Englewood Cliffs, NJ, 1987, p. 297.

stepz

strips