

| Signal Processing Toolbox |   |
Discrete prolate spheroidal sequences (Slepian sequences)
Syntax
[e,v]=dpss(n,nw) [e,v]=dpss(n,nw,k) [e,v]=dpss(n,nw,[k1 k2]) [e,v]=dpss(n,nw,'int') [e,v]=dpss(n,nw,'int',Ni) [e,v]=dpss(...,'trace')
Description
[e,v] = dpss(n,nw)
generates the first 2*nw discrete prolate spheroidal sequences (DPSS) of length n in the columns of e, and their corresponding concentrations in vector v. They are also generated in the DPSS MAT-file database dpss.mat. nw must be less than n/2.
[e,v] = dpss(n,nw,k)
returns the k most band-limited discrete prolate spheroidal sequences. k must be an integer such that 1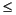
k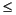
n.
[e,v] = dpss(n,nw,[k1 k2])
returns the k1st through the k2nd discrete prolate spheroidal sequences, where 1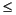
k1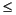
k2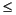
n.
|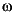
| 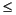
(2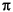
W), where W = nw/n is the half-bandwidth and 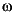 is in rad/sample.
is in rad/sample.
e(:,1) is the length n signal most concentrated in the frequency band |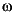
| 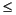
(2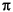
W) radians, e(:,2) is the signal orthogonal to e(:,1) that is most concentrated in this band, e(:,3) is the signal orthogonal to both e(:,1) and e(:,2) that is most concentrated in this band, etc.
nw are 2, 5/2, 3, 7/2, or 4.
[e,v] = dpss(n,nw,' uses the interpolation method specified by the string 'int')
int' to compute e and v from the sequences in dpss.mat with length closest to n. The string 'int' can be either:
spline': Use spline interpolation.
linear': Use linear interpolation. This is much faster but less accurate than spline interpolation.
[e,v] = dpss(n,nw,' interpolates from existing length int',Ni)
Ni sequences. The interpolation method 'linear' requires Ni > n.
[e,v] = dpss(...,' uses the trailing string trace')
'trace' to display which interpolation method DPSS uses. If you don't specify the interpolation method, the display indicates that you are using the direct method.
Example 1: Using dpss, dpssave, and dpssdir
Create a catalogue of 16 DPSS functions with nw = 4, and use spline interpolation on 10 of these functions while displaying the interpolation method you use. You can do this using dpss, dpsssave, and dpssdir:
% Create the catalogue of functions. [e,v] = dpss(16,4); % Save e and v in a MAT-file. dpsssave(4,e,v); % Find nw = 4. First create a structure called index. index = dpssdir; index.wlists ans = NW: 4 key: 1 % Use spline interpolation on 10 of the DPSS functions. [e1,v1] = dpss(10,4,'spline',size(e,1),'trace');
Example 2: Using dpss and dpssload
Create a set of DPSS functions using dpss, and use the spline method on a subset of these functions. Use dpssload to load the MAT-file created by dpss:
% Create the catalogue of functions. [e,v] = dpss(16,4); % Load dpss.mat, where e and v are saved. [e1,v1] = dpssload(16,4); % Use spline interpolation on 10 of the DPSS functions. [e1,v1] = dpss(10,4,'spline');
See Also
dpssclear, dpssdir, dpssload, dpsssave, pmtm
References
[1] Percival, D.B., and A.T. Walden. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge: Cambridge University Press, 1993.
 | downsample | dpssclear |  |