Partial Differential Equation Toolbox

The Error Indicator Function

The adaption is a feedback process. As such, it is easily applied to a larger range of problems than those for which its design was tailored. You want estimates, selection criteria, etc., to be optimal in the sense of giving the most accurate solution at fixed cost or lowest computational effort for a given accuracy. Such results have been proved only for model problems, but generally, the equidistribution heuristic has been found near optimal. Element sizes should be chosen such that each element contributes the same to the error. The theory of adaptive schemes makes use of a priori bounds for solutions in terms of the source function f. For nonelliptic problems such a bound may not exist, while the refinement scheme is still well defined and has been found to work well.

The error indicator function used in the toolbox is an element-wise estimate of the contribution, based on the work of C. Johnson et al. [5], [6]. For Poisson's equation -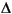u = f on 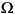, the following error estimate for the FEM-solution uh holds in the L2-norm || · ||:

|| (u - uh) || || hf || + Dh(uh)

where h = h(x) is the local mesh size, and

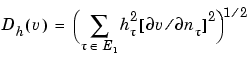
The braced quantity is the jump in normal derivative of v across edge , hr is the length of edge , and the sum runs over Ei, the set of all interior edges of the triangulation. The coefficients and are independent of the triangulation. This bound is turned into an element-wise error indicator function E(K) for element K by summing the contributions from its edges. The final form for the toolbox equation

- · (cu) + au = f

becomes

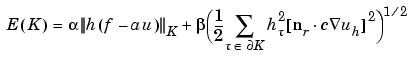
where n is the unit normal of edge and the braced term is the jump in flux across the element edge. The L2 norm is computed over the element K. This error indicator is computed by the pdejmps function.

Adaptive Mesh Refinement

The Mesh Refiner