Partial Differential Equation Toolbox

Diffusion

Since heat transfer is a diffusion process, the generic diffusion equation has the same structure as the heat equation:

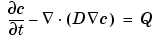
where c is the concentration, D is the diffusion coefficient and Q is a volume source. The diffusion process may be anisotropic, in which case D is a 2-by-2 matrix.

The boundary conditions can be of Dirichlet type, where the concentration on the boundary is specified, or of Neumann type, where the flux n · (D(c)) is specified. It is also possible to specify a generalized Neumann condition. It is defined by n· (D(c)) + qc = g, where q is a transfer coefficient.

Visualization of the concentration, its gradient, and the flux is available from the Plot Selection dialog box.

Heat Transfer

References