

| Partial Differential Equation Toolbox |   |
Conductive Media DC
For electrolysis and computation of resistances of grounding plates, we have a conductive medium with conductivity 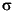 and a steady current. The current density J is related to the electric field E through J =
and a steady current. The current density J is related to the electric field E through J = 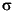 E. Combining the continuity equation
E. Combining the continuity equation  · J = Q, where Q is a current source, with the definition of the electric potential V yields the elliptic Poisson's equation
· J = Q, where Q is a current source, with the definition of the electric potential V yields the elliptic Poisson's equation
 · (
· (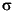
 V) = Q
V) = Q
The only two PDE parameters are the conductivity 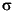 and the current source Q.
and the current source Q.
The Dirichlet boundary condition assigns values of the electric potential V to the boundaries, usually metallic conductors. The Neumann boundary condition requires the value of the normal component of the current density (n · (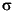
 (V))) to be known. It is also possible to specify a generalized Neumann condition defined by n · (
(V))) to be known. It is also possible to specify a generalized Neumann condition defined by n · (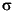
 (V) + qV = g, where q can be interpreted as a film conductance for thin plates.
(V) + qV = g, where q can be interpreted as a film conductance for thin plates.
The electric potential V, the electric field E, and the current density J are all available for plotting. Interesting quantities to visualize are the current lines (the vector field of J) and the equipotential lines of V. The equipotential lines are orthogonal to the current lines when 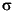 is isotropic.
is isotropic.
Example
Two circular metallic conductors are placed on a plane, thin conductor like a blotting paper wetted by brine. The equipotentials can be traced by a voltmeter with a simple probe, and the current lines can be traced by strongly colored ions, such as permanganate ions.
The physical model for this problem consists of the Laplace equation
 · (
· (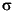
 V) = 0
V) = 0
for the electric potential V and the boundary conditions:
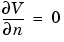
The conductivity 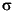 = 1 (constant).
= 1 (constant).
Using the Graphical User Interface
In the pdetool GUI, select the application mode Conductive Media DC and draw the blotting paper as a rectangle with corners in (-1.2,-0.6), (1.2,-0.6), (1.2,0.6), and (-1.2,0.6). Add two circles with radius 0.3 representing the circular conductors. Place them symmetrically with centers in (-0.6,0) and (0.6,0). If the rectangle's label is R1, and the circles' labels are C1 and C2, the 2-D domain of the problem is expressed by the set formula
Enter the set formula and click the  button to decompose the geometry and enter the boundary mode. Select all the outer boundaries and enter the Neumann boundary condition into the Boundary Condition dialog box. For the left circular conductor boundaries, enter the Dirichlet boundary condition V = 1, and for the right circular conductor, enter the Dirichlet condition V = -1.
button to decompose the geometry and enter the boundary mode. Select all the outer boundaries and enter the Neumann boundary condition into the Boundary Condition dialog box. For the left circular conductor boundaries, enter the Dirichlet boundary condition V = 1, and for the right circular conductor, enter the Dirichlet condition V = -1.
Next, open the PDE Specification dialog box and enter 0 into the edit box for the current source q. The default value for the conductivity 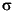 is 1 and needs not to be changed.
is 1 and needs not to be changed.
Initialize the mesh and refine it twice. End by jiggling the mesh once to improve the triangle quality.
Solve the PDE by clicking the = button. The resulting potential is zero along the y-axis, which is a vertical line of anti-symmetry for this problem.
Visualize the current density J by plotting the absolute value using a contour plot and the vector field using arrows. The current flows, as expected, from the conductor with a positive potential to the conductor with a negative potential.
The Current Density Between Two Metallic Conductors
 | AC Power Electromagnetics | Heat Transfer |  |