Partial Differential Equation Toolbox

Electrostatics

Applications involving electrostatics include high voltage apparatus, electronic devices, and capacitors. The "statics" implies that the time rate of change is slow, and that wavelengths are very large compared to the size of the domain of interest. In electrostatics, the electrostatic scalar potential V is related to the electric field E by E = -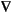V and, using one of Maxwell's equations, 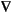· D = and the relationship D = 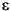E, we arrive at the Poisson equation

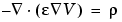
where 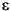is the coefficient of dielectricity and is the space charge density.

Note    should really be written as 0, where 0 is the coefficient of dielectricity or permittivity of vacuum (8.854 · 10-12 farad/meter) and is the relative coefficient of dielectricity that varies among different dielectrics (1.00059 in air, 2.24 in transformer oil, etc.).

Using the PDE Toolbox application mode Electrostatics, you can solve electrostatic problems modeled by the equation above.

The PDE Specification dialog box contains entries for 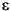and .

The boundary conditions for electrostatic problems can be of Dirichlet or Neumann type. For Dirichlet conditions, the electrostatic potential V is specified on the boundary. For Neumann conditions, the surface charge
n · (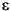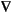V) is specified on the boundary.

For visualization of the solution to an electrostatic problem, the plot selections include the electrostatic potential V, the electric field E, and the electric displacement field D.

For a more in-depth discussion of problems in electrostatics, see [2].

Example

Let us consider the problem of determining the electrostatic potential in an air-filled quadratic "frame," bounded by a square with side length of 0.2 in the center and by outer limits with side length of 0.5. At the inner boundary, the electrostatic potential is 1000V. At the outer boundary, the electrostatic potential is 0V. There is no charge in the domain. This leads to the problem of solving the Laplace equation

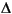• V = 0

with the Dirichlet boundary conditions V = 1000 at the inner boundary,
and V = 0 at the outer boundary.

Using the Graphical User Interface

After selecting the application mode Electrostatics, the 2-D area is most easily drawn by first drawing a square with sides of length 0.2 (use the Snap option and adjust the grid spacing if necessary). Then draw another square with sides of length 0.5 using the same center position. The 2-D domain is then simply SQ2-SQ1, if the first square is named SQ1 and the second square is named SQ2. Enter the expression into the Set formula edit box, and proceed to define the boundary conditions. Use Shift-click to select all the inner boundaries. Then double-click an inner boundary and enter 1000 as the Dirichlet boundary condition for the inner boundaries.

Next, open the PDE Specification dialog box, and enter 0 into the space charge density (rho) edit field. The coefficient of dielectricity can be left at 1, since it does not affect the result as long as it is constant.

Initialize the mesh, and click the = button to solve the equation. Using the adaptive mode, you can improve the accuracy of the solution by refining the mesh close to the reentrant corners where the gradients are steep. For example, use the triangle selection method picking the worst triangles and set the maximum number of triangles to 500. Add one uniform mesh refinement by clicking the Refine button once. Finally turn adaptive mode off, and click the = button once more.

To look at the equipotential lines, select a contour plot from the Plot Selection dialog box. To display equipotential lines at every 100th volt, enter 0:100:1000 into the Contour plot levels edit box.

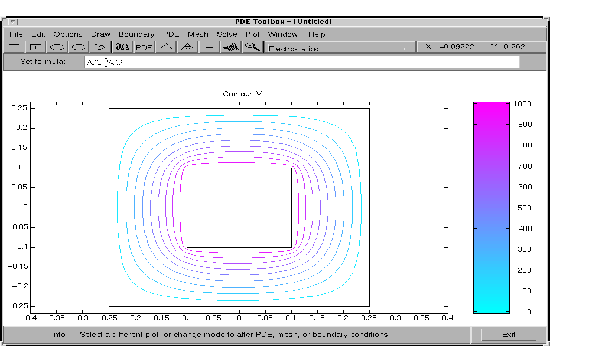
Equipotential Lines in Air-Filled Frame

Structural Mechanics -- Plane Strain

Magnetostatics