

| Partial Differential Equation Toolbox |   |
What Problems Can I Solve?
The basic equation of the PDE Toolbox is the PDE
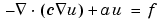
expressed in 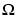 , which we shall refer to as the elliptic equation, regardless of whether its coefficients and boundary conditions make the PDE problem elliptic in the mathematical sense. Analogously, we shall use the terms parabolic equation and hyperbolic equation for equations with spatial operators like the one above, and first and second order time derivatives, respectively.
, which we shall refer to as the elliptic equation, regardless of whether its coefficients and boundary conditions make the PDE problem elliptic in the mathematical sense. Analogously, we shall use the terms parabolic equation and hyperbolic equation for equations with spatial operators like the one above, and first and second order time derivatives, respectively. 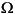 is a bounded domain in the plane. c, a, f, and the unknown u are scalar, complex valued functions defined on
is a bounded domain in the plane. c, a, f, and the unknown u are scalar, complex valued functions defined on 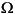 . c can be a 2-by-2 matrix function on
. c can be a 2-by-2 matrix function on  . The toolbox can also handle the parabolic PDE
. The toolbox can also handle the parabolic PDE
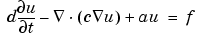 ,
,
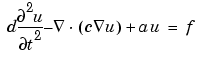 ,
,
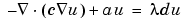
where d is a complex valued function on 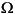 , and
, and 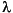 is an unknown eigenvalue. For the parabolic and hyperbolic PDE the coefficients c, a, f, and d can depend on time. A nonlinear solver is available for the nonlinear elliptic PDE
is an unknown eigenvalue. For the parabolic and hyperbolic PDE the coefficients c, a, f, and d can depend on time. A nonlinear solver is available for the nonlinear elliptic PDE
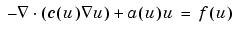
where c, a, and f are functions of the unknown solution u. All solvers can handle the system case
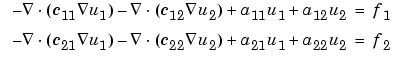
You can work with systems of arbitrary dimension from the command line. For the elliptic problem, an adaptive mesh refinement algorithm is implemented. It can also be used in conjunction with the nonlinear solver. In addition, a fast solver for Poisson's equation on a rectangular grid is available.
The following boundary conditions are defined for scalar u:
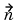 is the outward unit normal. g, q, h, and r are complex-valued functions defined on
is the outward unit normal. g, q, h, and r are complex-valued functions defined on 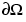 . (The eigenvalue problem is a homogeneous problem, i.e., g = 0, r = 0.) In the nonlinear case, the coefficients g, q, h, and r can depend on u, and for the hyperbolic and parabolic PDE, the coefficients can depend on time. For the two-dimensional system case, Dirichlet boundary condition is
. (The eigenvalue problem is a homogeneous problem, i.e., g = 0, r = 0.) In the nonlinear case, the coefficients g, q, h, and r can depend on u, and for the hyperbolic and parabolic PDE, the coefficients can depend on time. For the two-dimensional system case, Dirichlet boundary condition is
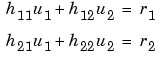
the generalized Neumann boundary condition is
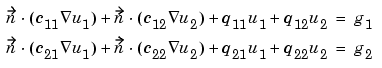
and the mixed boundary condition is
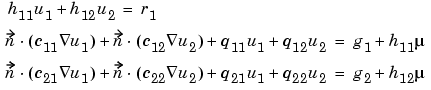 ,
,
where µ is computed such that the Dirichlet boundary condition is satisfied. Dirichlet boundary conditions are also called essential boundary conditions, and Neumann boundary conditions are also called natural boundary conditions. See The Finite Element Method, for the general system case.
 | Introduction | In Which Areas Can the Toolbox Be Used? |  |