Nonlinear Control Design Blockset

Solving the Optimization Problem

The Nonlinear Control Design Blockset transforms the constraints and simulated system output into an optimization problem of the form

where the boldface characters denote vectors. Variable x is a vectorization of the tunable variables while x_l and x_u are vectorizations of the lower and upper bounds on the tunable variables. The vector g(x) is a vectorization of the constraint bound error and w is a vectorization of weightings on the constraints. The scalar 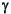imposes an element of slackness into the problem, which otherwise imposes that the goals be rigidly met (See the Appendix for more information).

Basically, the Nonlinear Control Design Blockset attempts to minimize the maximum (weighted) constraint error. The Nonlinear Control Design Blockset generates constraint errors at equally spaced time points (with spacing given by the Discretization interval defined in the Tunable Parameters dialog box) beginning at the simulation start time and ending at the simulation stop time. For upper bound constraints, we define the constraint error as the difference between the constraint boundary and the simulated output. For lower bound constraints, we define the constraint error as the difference between the simulated output and the constraint boundary.

This type of optimization problem is solved in the Optimization Toolbox routine constr. The routine uses a Sequential Quadratic Programming (SQP) method which solves a Quadratic Programming (QP) problem at each iteration. At each iteration, the routine updates an estimate of the Hessian of the Lagrangian. The line search is performed using a merit function. The routine uses an active set strategy for solving the QP subproblem.

For more information on the algorithm implemented by constr, see the Appendix or the Optimization Toolbox documentation.

Running the Optimization

Nonlinear Control Design Blockset Command-Line Interaction