Nonlinear Control Design Blockset

LQR Design for Inverted Pendulum

Chapters 2 and 4 contain examples of an inverted pendulum system. Both examples assume that an initial stabilizing LQR controller exists. This section details how that controller is generated.

Recall that, ignoring motor dynamics, the nonlinear equations of motion for the inverted pendulum system are

where:

f	Force applied to the cart by motor in Newtons Position of cart in meters
y	Angle of pendulum from vertical in radians
	Mass of cart (0.455kg)
M	Mass of pendulum (0.21kg)
l	Distance to center of mass of pendulum (i.e., one half its length of 0.61m
g	Acceleration of gravity (9.8m/s^2)

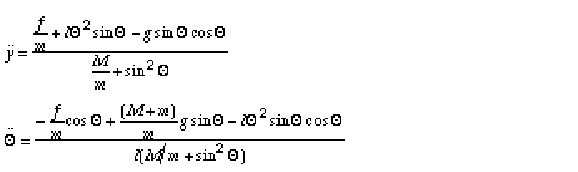
These equations may be linearized about the operating point y = 0 and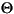
= 0 to yield the linear system

Using the MATLAB command

• Klqr = lqr(A,b,diag([0.25 0 4 0],0.003)
  

produces the stabilizing gain

• Klqr = [-28.8675 -28.5632 -145.0014 -14.8601]
  

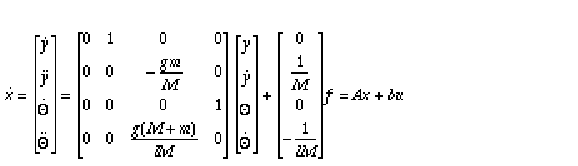
which is the initial stabilizing gain used in Chapters 2, "Tutorial" and 4, "Case Studies."

Nonlinear Control Design Blockset Global Variable ncdStruct