

| Model Predictive Control Toolbox |   |
Differences the states of a system and augments them with the output variables. Mainly used as a utility function for setting up model predictive controllers.
Syntax
Consider the process shown in the above block diagram. A state-space representation is:
where x is a vector of n state variables, u is a vector of nu manipulated variables, d is a vector of nd measured disturbances, w is a vector of nw unmeasured disturbances, y is a vector of ny plant outputs, z is measurement noise, and 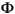 ,
, 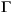 u,
u, 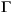 d,
d, 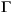 w, etc., are constant matrices of appropriate size. The variable
w, etc., are constant matrices of appropriate size. The variable 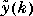 = Cx(k) represents the plant output before the addition of the direct contribution of the inputs [Duu(k) + Ddv(k) + Dww(k)] and the measurement noise [z(k)]. (The variable
= Cx(k) represents the plant output before the addition of the direct contribution of the inputs [Duu(k) + Ddv(k) + Dww(k)] and the measurement noise [z(k)]. (The variable 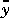 is the output before addition of the measurement noise). Define:
is the output before addition of the measurement noise). Define:
xa(k+1) = 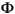 axa(k) +
axa(k) + 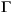 ua
ua 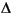 u(k) +
u(k) + 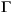 da
da 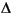 (k) +
(k) + 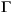 wa
wa 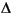 w(k)
w(k)
y(k) = Caxa(k) + Duu(k) + Ddd(k) + Dww(k) + z(k)
The mpcaugss function takes the matrices 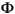 ,
, 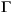 (= [
(= [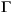 u
u 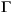 d
d 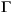 w]), C as input, and creates the augmented matrices
w]), C as input, and creates the augmented matrices 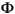 a,
a, 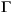 a, Ca and Da in the form shown above. The D input matrix is optional. If you include it,
a, Ca and Da in the form shown above. The D input matrix is optional. If you include it, mpcaugss assumes it has the form D = [Du Dd Dw]. If you omit it, the default is zero. Note that all MPC design routines require Du = Dd = 0.
The last output variable, na, is the order of the augmented system, i.e.,
na = n + ny. It is optional.
Example
The following system has 2 states, 3 inputs, and 2 outputs.
[phia,gama,ca,da,na]=mpcaugss(phi,gam,c)
phia =
0.8000 0 0 0
0 -0.2000 0 0
0.3200 0 1.0000 0
0 -0.3000 0 1.0000
gama =
1.0000 -1.0000 0
0 2.0000 -0.5000
0.4000 -0.4000 0
0 3.0000 -0.7500
ca =
0 0 1 0
0 0 0 1
da =
0 0 0
0 0 0
na =
4
 | mod2step, step format | mpccl |  |