| Model Browser User's Guide | |
Rols
This is the basic algorithm as described in Chen, Chng, and Alkadhimi [See References]. In Rols (Regularized Orthogonal Least Squares) the centers are chosen one at a time from a candidate set consisting of all the data points or a subset thereof. It picks new centers in a forward selection procedure. Starting from zero centers, at each step the center that reduces the regularized error the most is selected. At each step the regression matrix X is decomposed using the Gram-Schmidt algorithm into a product X = WB where W has orthogonal columns and B is upper triangular with ones on the diagonal. This is similar in nature to a QR decomposition. Regularized error is given by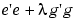 
where g = Bw and e is the residual, given by 
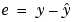. Minimizing regularized error makes the sum square error 
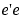small, while at the same time not letting 
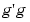get too large. As g is related to the weights by g = Bw, this has the effect of keeping the weights under control and reducing overfit. The term 
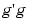rather than the sum of the squares of the weights 
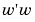is used to improve efficiency.
The algorithm terminates either when the maximum number of centers is reached, or adding new centers does not decrease the regularized error ratio significantly (controlled by a user-defined tolerance).
Fit Parameters
Maximum number of centers: The maximum number of centers that the algorithm can select. The default is the smaller of 25 centers or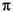 
of the number of data points. The format is min(nObs/4, 25). You can enter a value (for example, entering ten produces ten centers) or edit the existing formula (for example, (nObs/2, 25) produces half the number of data points or 25, whichever is smaller).
Percentage of data to be candidate centers: The percentage of the data points that should be used as candidate centers. This determines the subset of the data points that form the pool to select the centers from. The default is 100%, that is, to consider all the data points as possible new centers. This can be reduced to speed up the execution time.
Regularized error tolerance: Controls how many centers are selected before the algorithm stops. See Chen, Chng, and Alkadhimi [References] for details. This parameter should be a positive number between 0 and 1. Larger tolerances mean that fewer centers are selected. The default is 0.0001. If less than the maximum number of centers is being chosen, and you want to force the selection of the maximum number, then reduce the tolerance to epsilon (eps).
| | Fitting Routines | RedErr | |