Model Browser User's Guide

Constraint Types

Linear Constraints

You specify the coefficients of the equation for an (N-1) dimensional hyperplane in the N-factor space. The form of the equation is A.x = b where A is your defined coefficient vector, x is the vector of factor settings, and b is a scalar. The equation is applied by substituting design point settings (in coded values) for x. For example:

In two dimensions: A=(1, 2), x=(L, A), b=3

Then A.x = b expands to

1*L + 2*A = 3

Rearranging this, you can write it as

A = -L/2 + 3/2

which corresponds to the traditional equation of a 2-D straight line, y = mx + c, with m = -1/2 and c = 3/2. A.x = b is thus the higher dimensional extension of this equation.

The linear constraints work by selecting the region below the defined plane (that is, A.x <= b). To select a region above the plane, multiply all your values by -1: A -> -A, b -> -b.

For example, to select a simple plane where N<0.8 as a constraint boundary, enter 8 under N and set all the other factors to 0.

Ellipsoid Constraints

The ellipsoid constraint allows you to define an N-dimensional ellipsoid. You can specify the center of the ellipsoid, the length of each axis, and the rotation of the ellipsoid.

Ellipsoid center. .   You specify the center of the ellipsoid by entering values in the column marked Xc. These are the values, in coded units, that mark where you want the ellipsoid to be centered in each of the factor dimensions.

Axis length. .   You specify the size of the ellipsoid by entering values along the diagonal of the matrix to the right of Xc. The default values of 1 create an ellipsoid that touches the edge of the design space in each of the factor dimensions. Changing an entry to less than 1 extends the ellipsoid edge outside the design space along that factor axis (the extreme in this direction, 0, creates a cylinder). Changing an entry to greater than 1 contracts the ellipsoid edge to be inside the design space. In general, for an entry value X, the ellipsoid size in that factor is sqrt(1/X) times the size of the design space in that factor.

Rotation. .   The matrix entries that are not on the main diagonal control rotation of the ellipsoid.

The following example shows a defined ellipsoid constraint.

• You must enter values in the table to define the ellipsoid. If you leave the values at the defaults, the candidate set is a sphere.

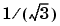• If you change a 1 to a 3, you reduce that axis to times its original size. A value of 2 reduces that axis to 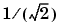, and so on.

The example above reduces the space available for the candidate set by a third in the A and N axes, forming an ellipsoid, as shown. A 3-D display of this constraint can be seen below.

1-D Table Constraints

1-D table constraints limit the maximum or minimum setting of one factor as a function of another factor. Linear interpolation between user-defined points is used to specify the constraint.

• You can select the appropriate factors to use.
• Move the large dots (by clicking them and dragging) to define a boundary. You must click the dots within the boundary of the space to select them. The following example shows a 1-D Table constraint. You can choose whether to constrain your design above or below the defined boundary using the Inequality drop-down menu.

  

2-D Table Constraints

2-D table constraints are an extension of the 1-D table. Constraint boundary values for a factor are specified over a 2-D grid of two other factors.

• You can specify these grid locations by entering values in the top row and left column, while the matrix of values for the third factor is entered in the rest of the edit boxes. To specify grid values, you can enter values directly or just choose the number of breakpoints for your grid and space them over the factors' ranges, using the controls decribed below.
• You can specify the number of breakpoints for the X and Y factors by using the buttons or typing directly into the edit boxes.
• You can click Span Range to space your breakpoints evenly over the range of X or Y. This is useful if you add some breakpoints as new points are often all at the maximum value for that factor. It is much easier to use the Span Range button than to change points manually.
• You can specify to keep the region below (<=) or above (>=) the constraint boundary, as for the 1-D table. Do this by choosing above or below from the Inequality drop-down menu for the Z factor.
• You can switch to coded values using the check box. See the example.

The constraint boundary between the defined grid points is calculated using bilinear interpolation.

• After defining any constraint, click OK. Your new constraint appears in the Constraint Manager list box. Click OK to return to the Design Editor, or Add to define more constraints.

  

A dialog appears if there are points in the design that fall outside your newly constrained candidate set. You can simply continue (delete them) or cancel the constraint. Fixed points are not removed by this process. For optimal designs you can also replace them with new random points within the new candidate set, as shown in the preceding example dialog.

Note    You only get the Replace points option for optimal designs. If you want to replace points removed by constraints from other designs, you can always use Edit -> Add Point to add points optimally, randomly, or at chosen places. However, if so many points have been removed by a constraint that there are not enough left to fit the current model, optimal addition is not possible. See Adding Design Points.

To view constraints:

1. Right-click the Design Editor display pane to reach the context menu.
2. Select Current View -> 3D Constraints. An example is shown.

   

These views are intended to give some idea of the region of space that is currently available within the constraint boundaries.

Applying Constraints

Importing Constraints