GARCH Toolbox

Initial Parameter Estimates

Although garchfit computes initial parameter estimates if you provide none, at times it may be helpful to compute and specify your own initial guesses to avoid convergence problems.

Note    If you specify initial estimates, you must provide complete conditional mean and/or variance model specifications. See the section Equality Constraints and Initial Parameter Estimates for more information.

Partial Estimation

An important property of a conditionally Gaussian innovations process is that the parameters of the conditional mean and the conditional variance are asymptotically uncorrelated (see Bollerslev [4], pages 315-317, Engle [8], pages 994-997, and Gourieroux, [11], pages 43-51). You can estimate initial parameter estimates of the mean separately from those of the variance, breaking the composite estimation process into two parts.

For example, if the conditional mean is an ARMAX model, you can first estimate the ARMAX parameters assuming a constant variance innovations process (i.e., a GARCH(0,0) conditional variance model). The sample variance of the estimated residuals is then an approximation of the unconditional variance of the innovations process {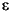_t}. Finally, based on reasonable parameter values of the GARCH and ARCH parameters of the conditional variance model, you can apply Eq. (2-7) to estimate the conditional variance constant .

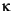For the common GARCH(1,1) model with Gaussian innovations,

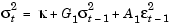
it often turns out that you can obtain reasonable initial estimates by assuming G₁ is approximately 0.8 to 0.9, and A₁ is approximately 0.05 to 0.10.

Iterative Estimation

Another approach is to estimate the complete model, examine the results, then modify the parameter estimates as initial guesses for another round of estimation. For example, suppose you have already estimated a composite ARMA(1,1)/GARCH(1,1) model.

• coeff
  coeff = 
           Comment: 'Mean: ARMAX(1,1,0); Variance: GARCH(1,1)'
                 R: 1
                 M: 1
                 P: 1
                 Q: 1
      Distribution: 'Gaussian'
                 C: 1.0000e-004
                AR: 0.5000
                MA: 0.4000
           Regress: []
                 K: 5.0000e-006
             GARCH: 0.4000
              ARCH: 0.5000
              FixC: []
             FixAR: []
             FixMA: []
        FixRegress: []
              FixK: []
          FixGARCH: []
           FixARCH: []
      Optimization: [1x1 struct]
  

As you examine the above coeff structure (i.e., the first output of garchfit), you may feel that the parameters of the ARMA(1,1) model appear reasonable. However, you suspect the GARCH(1,1) results may be stuck at a local maximum. You can modify the conditional variance parameters.

• coeff = garchset(coeff, 'K', 6.25e-6, 'GARCH', 0.85, 'ARCH', 0.05)
  coeff = 
           Comment: 'Mean: ARMAX(1,1,?); Variance: GARCH(1,1)'
                 R: 1
                 M: 1
                 P: 1
                 Q: 1
      Distribution: 'Gaussian'
                 C: 1.0000e-004
                AR: 0.5000
                MA: 0.4000
           Regress: []
                 K: 6.2500e-006
             GARCH: 0.8500
              ARCH: 0.0500
              FixC: []
             FixAR: []
             FixMA: []
        FixRegress: []
              FixK: []
          FixGARCH: []
           FixARCH: []
      Optimization: [1x1 struct]
  

You can then use this updated coeff specification structure as input to another round of optimization.

• [coeff, errors, LLF, innovations, sigma, summary] = 
  garchfit(coeff, xyz);
  

Compare the log-likelihood function values (i.e., LLF) to assess the various alternatives. This example illustrates the convenience of the shared specification structure.

Convergence Issues

Boundary Constraints and Statistical Inferences