GARCH Toolbox

Simplicity/Parsimony

Specify the smallest, most simplistic models that adequately describe your data. This is especially relevant for estimation. Simple models are easier to estimate, easier to forecast, and easier to analyze. In fact, certain model selection criteria, such as the AIC/BIC discussed in the section Model Selection and Analysis, penalize models for their complexity.

The section Analysis and Estimation Example Using the Default Model, examines the autocorrelation function (ACF) and partial autocorrelation function (PACF) of the XYZ Corporation. The results support the use of a simple constant for the conditional mean model as adequate to describe the data.

The following example illustrates an unnecessarily complicated model specification. It uses an ARMA(1,1)/GARCH(1,1) composite model, rather than a simple constant with GARCH(1,1) innovations, to estimate the model parameters for the returns of the XYZ Corporation.

Create a specification structure for an ARMA(1,1)/GARCH(1,1) model. Set the Display flag to off to suppress the optimization details that garchfit normally prints to the screen.

• spec = garchset;
  spec = garchset(spec, 'Display', 'off', 'R', 1, 'M', 1)
  spec = 
           Comment: 'Mean: ARMAX(1,1,?); Variance: GARCH(1,1)'
                 R: 1
                 M: 1
                 P: 1
                 Q: 1
      Distribution: 'Gaussian'
                 C: []
                AR: []
                MA: []
           Regress: []
                 K: []
             GARCH: []
              ARCH: []
              FixC: []
             FixAR: []
             FixMA: []
        FixRegress: []
              FixK: []
          FixGARCH: []
           FixARCH: []
      Optimization: [1x1 struct]
  

Now, estimate the model and examine the results.

• [coeff,errors,LLF,innovations,sigma,summary] = garchfit(spec, 
  xyz);
  garchdisp(coeff, errors)
   
    Number of Parameters Estimated: 6
  
                                 Standard          T     
    Parameter       Value          Error       Statistic 
   -----------   -----------   ------------   -----------
            C    0.00088504     0.00046465       1.9048
        AR(1)    -0.76595       0.098721        -7.7587
        MA(1)    0.80041        0.09305          8.6020
            K    7.9417e-007    2.7078e-007      2.9329
     GARCH(1)    0.96313        0.0051048      188.6716
      ARCH(1)    0.031735       0.0043606        7.2775
  

These results imply that the ARMA(1,1)/GARCH(1,1) composite model that best fits the observed data is

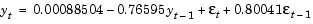
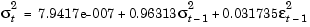
However, close examination of the conditional mean equation reveals that the AR(1) and MA(1) parameters are almost identical. In fact, rewriting the mean equation in backshift (i.e., lag) operator notation, where By_t = y_t-1,

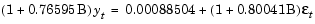
the auto-regressive and moving-average polynomials come close to canceling each other (see Box, Jenkins, Reinsel [7], pages 263-267). This is an example of parameter redundancy, or pole-zero cancellation. It implies that you can use the default model simple white noise process to approximate the conditional mean model.

In fact, from the section Analysis and Estimation Example Using the Default Model, the default model that best fits the observed data is

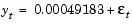
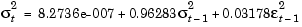
Note that the long-run (i.e., unconditional) mean and variance forecasts of each model are in very close agreement.

However, notice that the AR(1) and MA(1) T-statistics provide a misleading impression, implying that the parameters are highly significant. In fact, the more elaborate ARMA(1,1) model only complicates the analysis by requiring the estimation of two additional parameters. If you evaluate the information criteria, both AIC and BIC favor the default model (BIC is more decisive), and the LRT with two degrees-of-freedom fails to reject the default model.

Recommendations and Suggestions

Convergence Issues