Fuzzy Logic Toolbox

The Fuzzy Approach

It would be nice if we could just capture the essentials of this problem, leaving aside all the factors that could be arbitrary. If we make a list of what really matters in this problem, we might end up with the following rule descriptions.

• 1. If service is poor, then tip is cheap

  2. If service is good, then tip is average

  3. If service is excellent, then tip is generous

The order in which the rules are presented here is arbitrary. It doesn't matter which rules come first. If we wanted to include the food's effect on the tip, we might add the following two rules.

• 4. If food is rancid, then tip is cheap

  5. If food is delicious, then tip is generous

In fact, we can combine the two different lists of rules into one tight list of three rules like so.

• 1. If service is poor or the food is rancid, then tip is cheap

  2. If service is good, then tip is average

  3. If service is excellent or food is delicious, then tip is generous

These three rules are the core of our solution. And coincidentally, we've just defined the rules for a fuzzy logic system. Now if we give mathematical meaning to the linguistic variables (what is an "average" tip, for example?) we would have a complete fuzzy inference system. Of course, there's a lot left to the methodology of fuzzy logic that we're not mentioning right now, things like:

• How are the rules all combined?
• How do I define mathematically what an "average" tip is?

These are questions we provide detailed answers to in the next few chapters. The details of the method don't really change much from problem to problem -- the mechanics of fuzzy logic aren't terribly complex. What matters is what we've shown in this preliminary exposition: fuzzy is adaptable, simple, and easily applied.

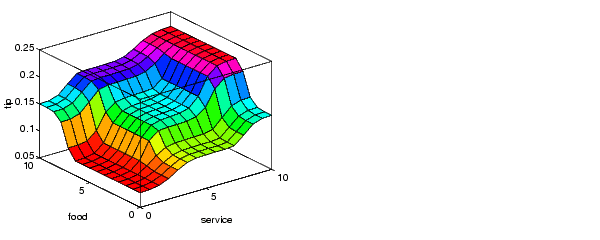
Here is the picture associated with the fuzzy system that solves this problem. The picture above was generated by the three rules above. The mechanics of how fuzzy inference works is explained Big Picture, Foundations of Fuzzy Logic, and in Fuzzy Inference Systems. In the Building Systems with the Fuzzy Logic Toolbox, the entire tipping problem is worked through using the graphical tools in the Fuzzy Logic Toolbox.

The Non-Fuzzy Approach

Observations