bdtsens (Financial Derivatives Toolbox)

Fixed income instrument prices and sensitivities by BDT interest rate tree

Syntax

[Delta, Gamma, Vega, Price] = bdtsens(BDTTree, InstSet, Options)

Arguments

BDTTree
Interest rate tree structure created by bdttree.

InstSet
Variable containing a collection of NINST instruments. Instruments are categorized by type; each type can have different data fields. The stored data field is a row vector or string for each instrument.

Options
(Optional) Derivatives pricing options structure created with derivset.

`BDTTree`	Interest rate tree structure created by `bdttree`.
`InstSet`	Variable containing a collection of `NINST` instruments. Instruments are categorized by type; each type can have different data fields. The stored data field is a row vector or string for each instrument.
Options	(Optional) Derivatives pricing options structure created with `derivset`.

Description

[Delta, Gamma, Vega, Price] = bdtsens(BDTTree, InstSet, Options) computes instrument sensitivities and prices for instruments using an interest rate tree created with bdttree. NINST instruments from a financial instrument variable, InstSet, are priced. bdtsens handles instrument types: 'Bond', 'CashFlow', 'OptBond', 'Fixed', 'Float', 'Cap', 'Floor', 'Swap'. See instadd for information on instrument types.

Delta is an NINST-by-1 vector of deltas, representing the rate of change of instrument prices with respect to changes in the interest rate. Delta is computed by finite differences in calls to bdttree. See bdttree for information on the observed yield curve.

Gamma is an NINST-by-1 vector of gammas, representing the rate of change of instrument deltas with respect to the changes in the interest rate. Gamma is computed by finite differences in calls to bdttree.

Vega is an NINST-by-1 vector of vegas, representing the rate of change of instrument prices with respect to the changes in the volatility 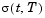. Vega is computed by finite differences in calls to bdttree. See bdtvolspec for information on the volatility process.

Note All sensitivities are returned as dollar sensitivities. To find the per-dollar sensitivities, divide by the respective instrument price.

Price is an NINST-by-1 vector of prices of each instrument. The prices are computed by backward dynamic programming on the interest rate tree. If an instrument cannot be priced, NaN is returned.

Delta and Gamma are calculated based on yield shifts of 100 basis points. Vega is calculated based on a 1% shift in the volatility process.

Examples

Load the tree and instruments from a data file. Compute delta and gamma for the cap and bond instruments contained in the instrument set.

load deriv.mat; 
BDTSubSet = instselect(BDTInstSet,'Type', {'Bond', 'Cap'}); 

instdisp(BDTSubSet)

Index Type CouponRate Settle        Maturity     Period  Name ...
1     Bond 0.1        01-Jan-2000   01-Jan-2003  1       10% Bond
2     Bond 0.1        01-Jan-2000   01-Jan-2004  2       10% Bond
     
Index Type Strike Settle      Maturity     CapReset...  Name ...  
3     Cap  0.15   01-Jan-2000 01-Jan-2004  1            15% Cap 
     
[Delta, Gamma] = bdtsens(BDTTree, BDTSubSet)

Warning: Not all cash flows are aligned with the tree. Result will 
be approximated.

Delta =

 -232.6681
 -281.0517
   78.3776

Gamma =

  1.0e+003 *

    0.8037
    1.1819
    0.7490

See Also

bdtprice, bdttree, bdtvolspec, instadd

bdtprice bdttimespec