| Filter Design Toolbox | |
Use a cascaded integrator-comb (CIC) decimation filter to decrease the sampling rate for a signal
Syntax
Description
y = cicdecimate(m,n,r,x,q)
filters the data in input vector x, applying a decimation factor (or sample rate reduction) r to the signal. r must be a positive integer. For example, when r = 5, the decimation filter reduces the signal length to one-fifth of the original length.
Input arguments m and n define the number of integrator and comb stages (n) and the number of differential delays (m) in the CIC decimation filter. Although m can be any positive integer, most often it is 1 or 2. Each integrator stage in the CIC filter comprises a single-pole infinite impulse response (IIR) filter with a unity feedback coefficient.
q represents a quantizer operating in signed fixed-point mode, as specified by the fixed keyword argument to the function quantizer.
cicdecimate uses the int32 data type for all arithmetic operations it performs while decimating the input signal. Limiting the data type to int32 means when the most significant bit (MSB) at the filter output is greater than 32, the overall sum can overflow causing the result to be wrong. When the MSB exceeds 32, cicdecimate generates a warning message that the MSB is too large.
With reference to the high sampling rate, the transfer function for the composite CIC filter is
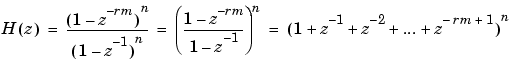
Design Considerations
When you design your CIC decimation filter, remember the following general points:
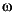= k * 2
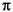/rm radians, k = 1,2,3....
n improves the filter ability to reject aliasing and imaging, but it also increases the droop (or rolloff) in the filter passband. Using an appropriate FIR filter in series after the CIC decimation filter can help you compensate for the induced droop.
Examples
This example applies a decimation factor r equal to 8 to a 160-point impulse signal. The signal output from the filter has 160/r, or 20, points or samples. Choosing 10 bits for the quantizer wordlength represents a fairly common setting for analog to digital converters. The plot shown after the code presents the stem plot of the decimated signal, with 20 samples remaining after decimation:
m = 4; % Differential delays in the filter n = 4; % filter stages r = 8 % decimation factor x = zeros(160,1); x(1) = 1; % Create a 160-point impulse signal q = quantizer([10 0],'fixed'); % Define the quantizer y = cicdecimate(m,n,r,x,q) stem(y) % Plot the output as a stem plot xlabel('Samples'); ylabel('Amplitude'); title('Decimated Signal');
This example demonstrates one way to compute the frequency response, using a 4-stage decimation filter with the decimation factor set to 7:
m = 1;n = 4; r = 7; % Define the filter parameters w = linspace(0,pi,1024); % Set the frequency in radians % Calculate the frequency response of the filter h = exp(i*n*w/2*(1-r*m)).*(sin(r*m*w/2)./sin(w/2)).^n; plot(w/pi,20*log10(abs(h))); grid on; xlabel('Normalized Frequency Relative to the High Sampling... Rate (\times\pi rad/sample)'); ylabel('Magnitude (dB)'); title('Frequency Response for the Example CIC... Decimation Filter');
Here's the frequency response plot for the filter. For details about the transfer function used to produce the frequency response, refer to [1] in the References section.
Algorithm
To show how the CIC decimation filter is constructed, the following figure presents a block diagram of the filter structure for a two-stage CIC decimation filter (n = 2). fs is the high sampling rate, the input to the decimation process.
See Also
References
[1] Hogenauer, E. B., "An Economical Class of Digital Filters for Decimation and Interpolation," IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-29(2): pp. 155-162, 1981
[2] Meyer-Baese, Uwe, "Hogenauer CIC Filters," in Digital Signal Processing with Field Programmable Gate Arrays, Springer, 2001, pp. 155-172
| | cell2sos | cicinterpolate | |
