DSP Blockset    
RLS Adaptive Filter

Compute filter estimates for an input using the RLS adaptive filter algorithm.

Library

Filtering / Adaptive Filters

Description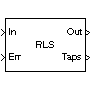

The RLS Adaptive Filter block recursively computes the least squares estimate (RLS) of the FIR filter coefficients.

The corresponding RLS filter is expressed in matrix form as

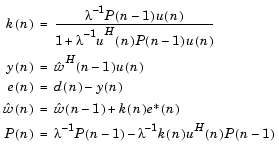
where 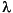-1 denotes the reciprocal of the exponential weighting factor. The variables are as follows

Variable
 Description
n
 The current algorithm iteration
u(n)
 The buffered input samples at step n
P(n)
 The inverse correlation matrix at step n
k(n)
 The gain vector at step n

The vector of filter-tap estimates at step n
y(n)
 The filtered output at step n
e(n)
 The estimation error at step n
d(n)
 The desired response at step n

The exponential memory weighting factor
.

The block icon has port labels corresponding to the inputs and outputs of the RLS algorithm. Note that inputs to the In and Err ports must be sample-based scalars. The signal at the Out port is a scalar, while the signal at the Taps port is a sample-based vector.

Block Ports
 Corresponding Variables
In

u, the scalar input, which is internally buffered into the vector u(n)
Out

y(n), the filtered scalar output

Err

e(n), the scalar estimation error
Taps

, the vector of filter-tap estimates

An optional Adapt input port is added when the Adapt input check box is selected in the dialog box. When this port is enabled, the block continuously adapts the filter coefficients while the Adapt input is nonzero. A zero-valued input to the Adapt port causes the block to stop adapting, and to hold the filter coefficients at their current values until the next nonzero Adapt input.

The implementation of the algorithm in the block is optimized by exploiting the symmetry of the inverse correlation matrix P(n). This decreases the total number of computations by a factor of two.

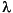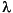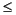
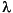
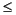
The FIR filter length parameter specifies the length of the filter that the RLS algorithm estimates. The Memory weighting factor corresponds to in the equations, and specifies how quickly the filter "forgets" past sample information. Setting =1 specifies an infinite memory; typically, 0.95 1.

The Initial value of filter taps specifies the initial value 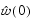as a vector, or as a scalar to be repeated for all vector elements. The initial value of P(n) is

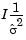
where 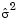is specified by the Initial input variance estimate parameter.

Example

The rlsdemo demo illustrates a noise cancellation system built around the RLS Adaptive Filter block.

Dialog Box

FIR filter length
The length of the FIR filter.
Memory weighting factor
The exponential weighting factor, in the range [0,1]. A value of 1 specifies an infinite memory. Tunable.
Initial value of filter taps
The initial FIR filter coefficients.
Initial input variance estimate
The initial value of 1/P(n).
Adapt input
Enables the Adapt port.

References

Haykin, S. Adaptive Filter Theory. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1996.

Supported Data Types

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Kalman Adaptive Filter
 DSP Blockset
LMS Adaptive Filter
 DSP Blockset

See Adaptive Filters for related information. Also see a list of all blocks in the Adaptive Filters library.


  Repeat RMS