

| DSP Blockset |   |
Implement the overlap-save method of frequency-domain filtering.
Library
Filtering / Filter Designs
Description
The Overlap-Save FFT Filter block uses an FFT to implement the overlap-save method, a technique that combines successive frequency-domain filtered sections of an input sequence.
Valid inputs to this block are 1-D vectors, sample-based vectors, frame-based vectors, and frame-based full matrices. All outputs are unbuffered into sample-based row vectors. The length of the output vector is equal to the number of channels in the input vector. An M-by-1 sample-based input has M channels, so it would result in a length-M sample-based output vector. An M-by-1 frame-based input has only one channel, so would result in a 1-by-1 (scalar) output.
The block's data output rate is M times faster than its data input rate, where M is the input frame-size. Thus, the block's data input and output rates are the same when the inputs are 1-D vectors, sample-based vectors, or frame-based row vectors. For frame-based column and frame-based full-matrix inputs, the block's data output rate is M times greater than the block's data input rate.
1-D vectors are treated as length-N sample-based vectors, and result in sample-based length-N row vectors.
Overlapping sections of input u are circularly convolved with the FIR filter coefficients
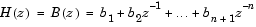
The numerator coefficients for H(z) are specified as a vector by the FIR coefficients parameter. The coefficient vector, b = [b(1) b(2) ... b(n+1)], can be generated by one of the filter design functions in the Signal Processing Toolbox, such as fir1. All filter states are internally initialized to zero.
If either the filter coefficients or the inputs to the block are complex, the Output parameter should be set to Complex. Otherwise, the default Output setting, Real, instructs the block to take only the real part of the solution.
The circular convolution of each section is computed by multiplying the FFTs of the input section and filter coefficients, and computing the inverse FFT of the product.
where nfft is specified by the FFT size parameter as a power-of-two value greater (typically much greater) than n+1. Values for FFT size that are not powers of two are rounded upwards to the nearest power-of-two value to obtain nfft.
The first n points of the circular convolution are invalid and are discarded. The Overlap-Save FFT Filter block outputs the remaining nfft-n points, which are equivalent to the linear convolution.
Latency
In single-tasking operation, the Overlap-Save FFT Filter block has a latency of nfft-n+1 samples. The first nfft-n+1 consecutive outputs from the block are zero; the first filtered input value appears at the output as sample nfft-n+2.
In multitasking operation, the Overlap-Save FFT Filter block has a latency of 2*(nfft-n+1) samples. The first 2*(nfft-n+1) consecutive outputs from the block are zero; the first filtered input value appears at the output as sample 2*(nfft-n)+3.
See Excess Algorithmic Delay (Tasking Latency) and "The Simulation Parameters Dialog Box" in the Simulink documentation for more information about block rates and the Simulink tasking modes.
Dialog Box
References
Oppenheim, A. V. and R. W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1989.
Proakis, J. and D. Manolakis. Digital Signal Processing. 3rd ed. Englewood Cliffs, NJ: Prentice-Hall, 1996.
Supported Data Types
To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.
See Also
| Overlap-Add FFT Filter |
DSP Blockset |
Also see Filtering for a list of all DSP Blockset filtering blocks.
 | Overlap-Add FFT Filter | Overwrite Values |  |