DSP Blockset

LDL Inverse

Compute the inverse of a Hermitian positive definite matrix using LDL factorization.

Library

Math Functions / Matrices and Linear Algebra / Matrix Inverses

Description

The LDL Inverse block computes the inverse of the Hermitian positive definite input matrix S by performing an LDL factorization.

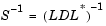
L is a lower triangular square matrix with unity diagonal elements, D is a diagonal matrix, and L^* is the Hermitian (complex conjugate) transpose of L. Only the diagonal and lower triangle of the input matrix are used, and any imaginary component of the diagonal entries is disregarded. The output is always sample-based.

LDL factorization requires half the computation of Gaussian elimination (LU decomposition), and is always stable. It is more efficient than Cholesky factorization because it avoids computing the square roots of the diagonal elements.

The algorithm requires that the input be Hermitian positive definite. When the input is not positive definite, the block reacts with the behavior specified by the Non-positive definite input parameter. The following options are available:

• Ignore -- Proceed with the computation and do not issue an alert. The output is not a valid inverse.
• Warning -- Display a warning message in the MATLAB command window, and continue the simulation. The output is not a valid inverse.
• Error -- Display an error dialog box and terminate the simulation.

Dialog Box

Non-positive definite input

Response to non-positive definite matrix inputs. Tunable.

References

Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Supported Data Types

• Double-precision floating point
• Single-precision floating point

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

See Also

Cholesky Inverse	DSP Blockset
LDL Factorization	DSP Blockset
LDL Solver	DSP Blockset
LU Inverse	DSP Blockset
Pseudoinverse	DSP Blockset
inv	MATLAB

See Inverting Matrices for related information. Also see Matrix Inverses for a list of all the blocks in the Matrix Inverses library.

LDL Factorization

LDL Solver