Communications Blockset

Evaluating Results

Generating a bit error rate curve requires multiple simulations. You can perform multiple simulations from the command line using the sim command. To do this:

• Change the value of the Es/No parameter in the AWGN Channel block mask from a constant to the variable EsNodB.
• Run the following code to generate the data for plotting the BER curve.

• CodeRate = 0.75;
  EbNoVec = [2:.2:10];
  EsNoVec = EbNoVec + 10*log10(CodeRate);
  BERVec = zeros(length(EsNoVec),3);
  for n=1:length(EsNoVec),
      EsNodB = EsNoVec(n);
      sim('tstconvcod');
      BERVec(n,:) = BER_Data;
  end
  

To confirm the validity of the results, compare them to an established performance bound. The bit error rate performance of a rate 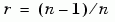punctured code is bounded above by the expression

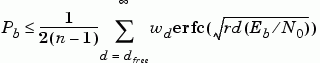
In this expression, erfc denotes the complementary error function, r is the code rate, and both d_free and w_d are dependent on the particular code. For the rate 3/4 code of this example, d_free = 5, w₅ = 42, w₆ = 201, w₇ = 1492, and so on. See reference [1] for more details.

The following commands compute an approximation of this bound in MATLAB using the first seven terms of the summation.

• dist = [5:11];
  nerr = [42 201 1492 10469 62935 379644 2253373];
  CodeRate = 3/4;
  EbNo_dB = [2:.02:10];
  EbNo = 10.0.^(EbNo_dB/10);
  arg = sqrt(CodeRate*EbNo'*dist);
  bound = nerr*(1/6)*erfc(arg)';
  

The figure below shows simulation results and bounds for the rate 3/4 punctured code in this example, as well as other punctured codes of rates 2/3 and 7/8 derived from the same original constraint length 7 rate 1/2 code. The puncture patterns for these other rates are listed in reference [1]. The simulations used to generate the data for this plot were set to stop after 1000 errors or 40 million bits, whichever came first.

In each case, the results agree well with the theoretical bounds. In some cases, at the lower bit error rates, the simulation results appear to indicate error rates slightly above the bound. This is not a result of simulation variance, since over 500 bit errors were observed at even the lowest bit error rate value. Rather, this is a result of the finite traceback depth in the decoder.

Calculating the Error Rate

Bibliography