OVSF Code Generator (Communications Blockset)

Generate an orthogonal variable spreading factor (OVSF) code from a set of orthogonal codes

Library

Spreading Codes

Description

The OVSF Code Generator block generates an OVSF code from a set of orthogonal codes. OVSF codes were first introduced for 3G communication systems. OVSF codes are primarily used to preserve orthogonality between different channels in a communication system.

OVSF codes are defined as the rows of an 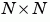matrix, C_N, which is defined recursively as follows. First, define C₁ = [1]. Next, assume that C_N is defined and let C_N(k) denote the kth row of C_N. Define C_2N by

Note that C_Nis only defined for N a power of 2. It follows by induction that the rows of C_Nare orthogonal.

The OVSF codes can also be defined recursively by a tree structure, as shown in the following figure.

If [C] is a code length 2^r at depth r in the tree, where the root has depth 0, the two branches leading out of C are labeled by the sequences [C C] and [C -C], which have length 2^r+1. The codes at depth r in the tree are the rows of the matrix C_N, where N = 2^r.

Note that two OVSF codes are orthogonal if and only if neither code lies on the path from the other code to the root. Since codes assigned to different users in the same cell must be orthogonal, this restricts the number of available codes for a given cell. For example, if the code C₄₁ in the tree is assigned to a user, the codes C₁₀, C₂₀, C₈₂, C₈₃, and so on, cannot be assigned to any other user in the same cell.

Block Parameters

You specify the code the OVSV Code Generator block outputs by two parameters in the block's mask: the Spreading factor, which is the length of the code, and the Code index, which must be an integer in the range
[0, 1, ... , N - 1], where N is the spreading factor. If the code appears at depth r in the preceding tree, the Spreading factor is 2^r. The Code index specifies how far down the column of the tree at depth r the code appears, counting from 0 to N - 1. For C_{N, k} in the preceding diagram, N is the Spreading factor and k is the Code index.

You can recover the code from the Spreading factor and the Code index as follows. Convert the Code index to the corresponding binary number, and then add 0s to the left, if necessary, so that the resulting binary sequence x₁ x₂ ... x_r has length r, where r is the logarithm base 2 of the Spreading factor. This sequence describes the path from the root to the code. The path takes the upper branch from the code at depth i if x_i = 0, and the lower branch if x_i = 1.

To reconstruct the code, recursively define a sequence of codes C_i for as follows. Let C₀ be the root [1]. Assuming that C_i has been defined, for i < r, define C_i+1 by

The code C_N has the specified Spreading factor and Code index.

For example, to find the code with Spreading factor 16 and Code index 6, do the following:

Convert 6 to the binary number 110.
Add one 0 to the left to obtain 0110, which has length 4 = log₂ 16.
Construct the sequences C_i according to the following table.

i
x_i
C_i

0

C₀ = [1]

1
0
C₁ = C₀ C₀ = [1] [1]

2
1
C₂ = C₁ -C₁ = [1 1] [-1 -1]

3
1
C₃ = C₂ -C₂ = [1 1 -1 -1] [-1 -1 1 1]

4
0
C₄ = C₃ C₃ = [1 1 -1 -1 -1 -1 1 1] [1 1 -1 -1 -1 -1 1 1]

i	x_i	C_i
0		C₀ = [1]
1	0	C₁ = C₀ C₀ = [1] [1]
2	1	C₂ = C₁ -C₁ = [1 1] [-1 -1]
3	1	C₃ = C₂ -C₂ = [1 1 -1 -1] [-1 -1 1 1]
4	0	C₄ = C₃ C₃ = [1 1 -1 -1 -1 -1 1 1] [1 1 -1 -1 -1 -1 1 1]

The code C₄has Spreading factor 16 and Code index 6.

Dialog Box

Spreading factor: Positive integer that is a power of 2, specifying the length of the code.
Code index: Integer in the range [0, 1, ... , N - 1] specifying the code, where N is the Spreading factor.
Sample time: A positive real scalar specifying the sample time of the output signal.
Frame-based outputs: Determines whether the output is frame-based or sample-based.
Samples per frame: The number of samples in a frame-based output signal. This field is active only if you select the Frame-based outputs check box.

OQPSK Modulator Passband Phase/Frequency Offset