Kasami Sequence Generator (Communications Blockset)

Generate a Kasami sequence from the set of Kasami sequences

Library

Sequence Generators sublibrary of Comm Sources

Description

The Kasami Sequence Generator block generates a sequence from the set of Kasami sequences. The Kasami sequences are a set of sequences that have good cross-correlation properties.

There are two classes of Kasami sequences: the small set and the large set. The large set contains all the sequences in the small set. Only the small set is optimal in the sense of matching Welch's lower bound for correlation functions.

Kasami sequences have period N = 2ⁿ - 1, where n is a nonnegative, even integer. Let u be a binary sequence of length N, and let w be the sequence obtained by decimating u by 2^n/2 +1. The small set of Kasami sequences is defined by the following formulas, in which T denotes the left shift operator, m is the shift parameter for w, and 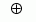denotes addition modulo 2.

Figure 2-1: Small Set of Kasami Sequences for n Even

Note that the small set contains 2^n/2 sequences.

For mod(n, 4) = 2, the large set of Kasami sequences is defined as follows. Let v be the sequence formed by decimating the sequence u by 2^{n/2 + 1}+ 1. The large set is defined by the following table, in which k and m are the shift parameters for the sequences v and w, respectively.

Figure 2-2: Large Set of Kasami Sequences for mod(n, 4) = 2

The sequences described in the first three rows of the preceding figure correspond to the Gold sequences for mod(n, 4) = 2. See the reference page for the Gold Sequence Generator block for a description of Gold sequences. However, the Kasami sequences form a larger set than the Gold sequences.

The correlation functions for the sequences takes on the values
{-t(n), -s(n), -1, s(n) -2 , t(n) - 2}, where

and

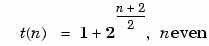
Block Parameters

The Generator polynomial parameter specifies the generator polynomial, which determines the connections in the shift register that generates the sequence u. You can specify the Generator polynomial parameter using either of these formats:

A vector that lists the coefficients of the polynomial in descending order of powers. The first and last entries must be 1. Note that the length of this vector is one more than the degree of the generator polynomial.
A vector containing the exponents of z for the nonzero terms of the polynomial in descending order of powers. The last entry must be 0.

For example, [1 0 0 0 0 0 1 0 1] and [8 2 0] represent the same polynomial, .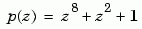

The Initial states parameter specifies the initial states of the shift register that generates the sequence u. Initial States is a binary scalar or row vector of length equal to the degree of the Generator polynomial. If you choose a binary scalar, the block expands the scalar to a row vector of length equal to the degree of the Generator polynomial, all of whose entries equal the scalar.

The Sequence index parameter specifies the shifts of the sequences v and w used to generate the output sequence. You can specify the parameter in either of two ways:

To generate sequences from the small set, for n is even, you can specify the Sequence index as an integer m. The range of m is [-1, ..., 2^n/2 - 2]. The following table describes the output sequences corresponding to Sequence index m:

Sequence Index
Range of Indices
Output Sequence

-1
m = -1
u

m
m = 0, ... , 2^n/2 - 2

Sequence Index	Range of Indices	Output Sequence
`-1`	m = -1	u
`m`	m = 0, ... , 2^n/2 - 2

To generate sequences from the large set, for mod (n, 4) = 2, where n is the degree of the Generator polynomial, you can specify Sequence index as an integer vector [k m]. In this case, the output sequence is from the large set. The range for k is [-2, ..., 2ⁿ - 2], and the range for m is [-1, ..., 2^n/2 - 2]. The following table describes the output sequences corresponding to Sequence index [k m]:


Sequence Index [k m]	Range of Indices	Output Sequence
`[-2 -1]`	k = -2, m = -1	u
`[-1 -1]`	k = -1, m = -1	v
`[k -1]`	k = 0, 1, ... , 2ⁿ - 2 m = -1
`[-2 m]`	k = -2 m = 0, 1, ..., 2^n/2 - 2
`[-1 m]`	k = -1 m = 0, ... , 2^n/2 - 2
`[k m]`	k = 0, ... , 2ⁿ - 2 m = 0, ... , 2^n/2 - 2

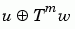You can shift the starting point of the Gold sequence with the Shift parameter, which is an integer representing the length of the shift.

You can use an external signal to reset the values of the internal shift register to the initial state by selecting the Reset on nonzero input check box. This creates an input port for the external signal in the Kasami Sequence Generator block. The way the block resets the internal shift register depends on whether its output signal and the reset signal are sample-based or frame-based. See Example: Resetting a Signal for an example.

Polynomials for Generating Kasami Sequences

The following table lists some of the polynomials that you can use to generate the Kasami set of sequences.

n
N
Polynomial
Set

4
15
[4 1 0]
Small

6
63
[6 1 0]
Large

8
255
[8 4 3 2 0]
Small

10
1023
[10 3 0]
Large

12
4095
[12 6 4 1 0]
Small

n	N	Polynomial	Set
4	15	[4 1 0]	Small
6	63	[6 1 0]	Large
8	255	[8 4 3 2 0]	Small
10	1023	[10 3 0]	Large
12	4095	[12 6 4 1 0]	Small

Dialog Box

Generator polynomial: Binary vector specifying the generator polynomial for the sequence u.
Initial states: Binary scalar or row vector of length equal to the degree of the Generator polynomial, which specifies the initial states of the shift register that generates the sequence u.
Sequence index: Integer or vector specifying the shifts of the sequences v and w used to generate the output sequence.
Shift: Integer scalar that determines the offset of the Kasami sequence from the initial time.
Sample time: Period of each element of the output signal.
Frame-based outputs: Determines whether the output is frame-based or sample-based.
Samples per frame: The number of samples in a frame-based output signal. This field is active only if you select the Frame-based outputs check box.
Reset on nonzero input: When selected, you can specify an input signal that resets the internal shift registers to the original values of the Initial states.

Reference

[1] Peterson and Weldon, Error Correcting Codes, 2nd Ed., MIT Press, Cambridge, MA, 1972.

[2] Proakis, John G., Digital Communications, Third edition, New York, McGraw Hill, 1995.

[3] Sarwate, D. V. and Pursley, M.B., "Crosscorrelation Properties of Pseudorandom and Related Sequences," Proc. IEEE, Vol. 68, No. 5, May 1980, pp. 583-619.

I/Q Imbalance Linearized Baseband PLL