Communications Toolbox

Noncausality and the Group Delay Parameter

Without propagation delays, both Hilbert filters and raised cosine filters are noncausal. This means that the current output depends on the system's future input. In order to design only realizable filters, the hilbiir, rcosine, and rcosflt functions delay the input signal before producing an output. This delay, known as the filter's group delay, is the time between the filter's initial response and its peak response. The group delay is defined as

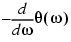
where 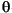is the phase of the filter and 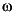is the frequency in radians. This delay is set so that the impulse response before time zero is negligible and can safely be ignored by the function.

For example, the Hilbert filter whose impulse is shown below uses a group delay of 1 second. Notice in the figure that the impulse response near time 0 is small and that the large impulse response values occur near time 1.

Impulse Response of a Hilbert Filter

Example: Compensating for Group Delays When Analyzing Data

Comparing filtered with unfiltered data might be easier if you delay the unfiltered signal by the filter's group delay. For example, suppose you use the code below to filter x and produce y.

• tx = 0:4; % Times for data samples
  x = [0 1 1 1 1]'; % Binary data samples
  % Filter the data and use a delay of 2 seconds.
  delay = 2;
  [y,ty] = rcosflt(x,1,8,'fir',.3,delay);
  

Here, the elements of tx and ty represent the times of each sample of x and y, respectively. However, y is delayed relative to x, so corresponding elements of x and y do not have the same time values. Plotting y against ty and x against tx is less useful than plotting y against ty and x against a delayed version of tx.

• % Top plot
  subplot(2,1,1), plot(tx,x,'*',ty,y);
  % Bottom plot delays tx.
  subplot(2,1,2), plot(tx+delay,x,'*',ty,y);
  

For another example of compensating for group delay, see the raised-cosine filter demo by typing playshow rcosdemo.

Special Filters

Designing Hilbert Transform Filters