

| Aerospace Blockset |   |
Implement an Euler angle representation of six-degrees-of-freedom equations of motion
Library
Description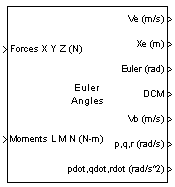
The 6DoF (Euler Angles) block considers the rotation of a body-fixed coordinate frame 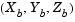 about an Earth-fixed reference frame
about an Earth-fixed reference frame 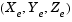 . The origin of the body-fixed coordinate frame is the center of gravity of the body, and the body is assumed to be rigid, an assumption that eliminates the need to consider the forces acting between individual elements of mass. The Earth-fixed reference frame is considered inertial, a simplification that allows the forces due to the Earth's motion relative to a star-fixed reference system to be neglected.
. The origin of the body-fixed coordinate frame is the center of gravity of the body, and the body is assumed to be rigid, an assumption that eliminates the need to consider the forces acting between individual elements of mass. The Earth-fixed reference frame is considered inertial, a simplification that allows the forces due to the Earth's motion relative to a star-fixed reference system to be neglected.
The translational motion of the body-fixed coordinate frame is given below, where the applied forces [Fx Fy Fz]T are in the body-fixed frame, and the mass of the body 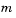 is assumed constant.
is assumed constant.
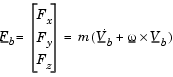
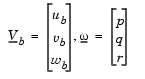
The rotational dynamics of the body-fixed frame are given below, where the applied moments are [L M N]T, and the inertia tensor 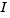 is with respect to the origin O.
is with respect to the origin O.
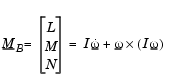
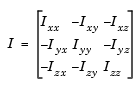
The relationship between the body-fixed angular velocity vector, [p q r]T, and the rate of change of the Euler angles, [ 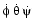 ]T, can be determined by resolving the Euler rates into the body-fixed coordinate frame.
]T, can be determined by resolving the Euler rates into the body-fixed coordinate frame.
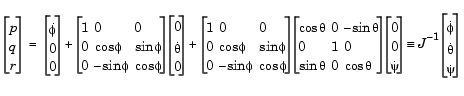
Inverting 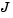 then gives the required relationship to determine the Euler rate vector.
then gives the required relationship to determine the Euler rate vector.
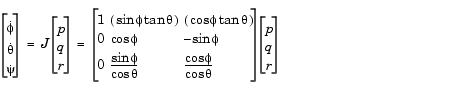
Dialog Box
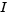 , in kilograms meters squared.
, in kilograms meters squared.Inputs and Outputs
The first input to the block is a vector containing the three applied forces, in Newtons, and the second input is a vector containing the three applied moments, in Newton meters.
The first output is a three-element vector containing the velocity in the Earth-fixed reference frame, in meters per second.
The second output is a three-element vector containing the position in the Earth-fixed reference frame, in meters.
The third output is a three-element vector containing the Euler rotation angles [roll, pitch, yaw], in radians.
The fourth output is a 3-by-3 matrix for the coordinate transformation from Earth-fixed axes to body-fixed axes.
The fifth output is a three-element vector containing the velocity in the body-fixed frame, in meters per second.
The sixth output is a three-element vector containing the angular rates in body-fixed axes, in radians per second.
The seventh output is a three-element vector containing the angular accelerations in body-fixed axes, in radians per second.
Assumptions and Limitations
The block assumes that the applied forces are acting at the center of gravity of the body, and that the mass and inertia are constant.
See Also
 | 6DoF Animation | 6DoF (Quaternion) |  |