quad, quad8 (MATLAB Functions)

Numerically evaluate integral, adaptive Simpson quadrature

Note The quad8 function, which implemented a higher order method, is obsolete. The quadl function is its recommended replacement.

Syntax

q = quad(fun,a,b)
q = quad(fun,a,b,tol)
q = quad(fun,a,b,tol,trace)
q = quad(fun,a,b,tol,trace,p1,p2,...)
[q,fcnt] = quadl(fun,a,b,...)

Description

Quadrature is a numerical method used to find the area under the graph of a function, that is, to compute a definite integral.

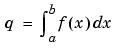
q = quad(fun,a,b) approximates the integral of function fun from a to b to within an error of 10^-6 using recursive adaptive Simpson quadrature. fun accepts a vector x and returns a vector y, the function fun evaluated at each element of x.

q = quad(fun,a,b,tol) uses an absolute error tolerance tol instead of the default which is 1.0e-6. Larger values of tol result in fewer function evaluations and faster computation, but less accurate results. In MATLAB version 5.3 and earlier, the quad function used a less reliable algorithm and a default relative tolerance of 1.0e-3.

q = quad(fun,a,b,tol,trace) with non-zero trace shows the values of [fcnt a b-a Q] during the recursion.

q = quad(fun,a,b,tol,trace,p1,p2,...) provides for additional arguments p1,p2,... to be passed directly to function fun, fun(x,p1,p2,...). Pass empty matrices for tol or trace to use the default values.

[q,fcnt] = quad(...) returns the number of function evaluations.

The function quadl may be more efficient with high accuracies and smooth integrands.

Examples

The function fun can be

An inline object

F = inline('1./(x.^3-2*x-5)'); 
Q = quad(F,0,2);

A function handle

```
Q = quad(@myfun,0,2); 
```

where myfun.m is an M-file.

function y = myfun(x) 
y = 1./(x.^3-2*x-5);

Algorithm

quad implements a low order method using an adaptive recursive Simpson's rule.

Diagnostics

quad may issue one of the following warnings:

'Minimum step size reached' indicates that the recursive interval subdivision has produced a subinterval whose length is on the order of roundoff error in the length of the original interval. A nonintegrable singularity is possible.

'Maximum function count exceeded' indicates that the integrand has been evaluated more than 10,000 times. A nonintegrable singularity is likely.

'Infinite or Not-a-Number function value encountered' indicates a floating point overflow or division by zero during the evaluation of the integrand in the interior of the interval.

See Also

dblquad, inline, quadl, triplequad, @ (function handle)

References

[1] Gander, W. and W. Gautschi, "Adaptive Quadrature - Revisited", BIT, Vol. 40, 2000, pp. 84-101. This document is also available at http:// www.inf.ethz.ch/personal/gander.

qrupdate quadl