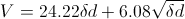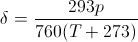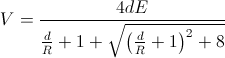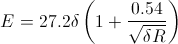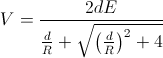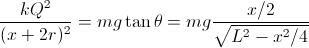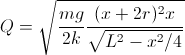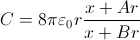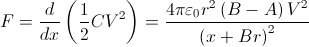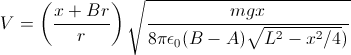In this page I will describe some experiments about high-voltage measurements in my electrostatic machines and other devices, using measuring instruments built by me. Initially I describe a spark gap voltmeter, Henley's electrometer, and a pith ball electroscope and comment on how to calibrate the meters for more precise measurements.

Sphere gap meter

Uniform field spark gap

Spark gaps formed by parallel plates, dimensioned so the field at the center of the plates is approximately uniform and maximum, spark when the electric field at the gap is close to 30 kV/cm, in normal atmospheric conditions. In [2] there is a long discussion about behavior of spark gaps, with formulas due to various researchers that approximate the breakdown voltage as function of the gap spacing. It's well known also that the air pressure and temperature affect the breakdown voltage. Another effect is that the electric field required for breakdown in small gaps is larger than in the case of large gaps. From the discussion there, a good formula for this case, which also appears in [3], can be:


V is the breakdown in kV, d the gap space in cm, and δ is a correction factor for pressure and temperature, with p the pressure in torr (mm Hg) and T the temperature in degrees Celsius. It reduces to 1 at sea level and 20 °C:


Sphere spark gap

A classical method for high-voltage measurement is a sphere spark gap, also object of many studies in the past, as it was for long time the most practical way to measure high voltages. Several formulas and tables for the relation between the geometry of the system and the sparking voltage can be found. This measuring method is considered precise within a few per cent, if enough care is taken. I found convenient to use the formulas that can be found in reference [1] (the first appears in [3] and [6] too, and comes from [7] ). For two balls, not grounded (symmetrically charged to ±V/2), the breakdown voltage is:

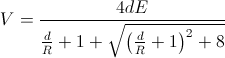
where V is in kV,  d is the gap distance in cm, R is the radius of the spheres, and E is the electric field at the surface or one sphere that causes breakdown (V/cm). The value of E is around 30 kV/cm in air, but it varies with the geometry, pressure, and temperature. A better expression for E for a sphere gap is (kV/cm):

The correction term δ is the same listed above. The formula for V is an approximation, since there is no simple solution for the electric field on a two-spheres configuration. The exact value can be calculated by a series, however, and is very close to this approximation. The second formula says that the breakdown field depends on the radius of the spheres, and is an empirical simplification of the quite complicated exact behavior of a sphere spark gap.

In [1] there is also a formula for the case of one grounded sphere, which the author says that does not work well due to interference of the supports of the spheres, greater in this case. Really, the formula predicts values a bit smaller than the correct values from the exact solution even between two ideal spheres.

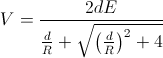
The first formula gives a value of  V = dE when R>>d and V = 2RE when d>>R, meaning that both spheres start to produce corona. The last formula also gives V = dE in the first case, but gives V = dR in the last, meaning that just one sphere produces corona.

I made a sphere gap with two 3.4 cm hollow copper spheres mounted on a support where their separation can be varied and measured by a ruler. Spheres of other sizes, the same that I use for terminals of electrostatic machines, can be used too. The system used, supporting the balls in parallel insulators, is not the best because the supports interfere in the electric field shaping for long sparks and even produce some corona, but I found that at least up to 25 kV the gap meter as built works correctly. A more precise distance meter could be used too, as the simple ruler gives a precision of 0.25 mm at most. In the picture above, the device can be seen, connected in parallel with a Leyden jar and an insulated Henley electrometer. The connections are not critical, and wires with loops at the ends and a ball chain are enough. One ball is grounded at the wooden table and the other connected to the device to be measured, which in that case was a small electrostatic machine.

The curves below show a comparison between these formulas and my measurements, for T = 26 °C and p = 685 mm Hg, for distances d between 0.2 and 0.9 cm, with the vertical scale in kV. "vmed" are the experimental values. "v30k" the values assuming E = 30 kV/cm, "v760" the values assuming 20 °C and 760 mm Hg, "v685" the values for the experimental conditions, and "vg685" the corresponding values using the formula for one grounded sphere. Most of the experimental values are between the two last curves, as they should be.

Sphere gap measurements and calculations

   
Henley's electrometers

Henley's electrometer [4] is a simple repulsion electrometer. It has a wooden rod with a ball at the top and a metal ferrule at the bottom, which has a pin that can be fixed on a base or on other devices. A light ball is suspended at the center of an angular scale through a light stick. When connected to high voltage, the ball is repelled from the vertical support, and the angle is a measurement of the voltage. I made several, some of them shown above. The first is smaller and more sensitive. The second has a guard to reduce the effect of the scale repelling or attracting the index [5]. The third has a better support for the index, more similar to the system used in the old instruments and that allows free movement even with the repulsion between the scale and the index. The index was fixed in a hole in a short brass cylinder with point bearings at both ends, one of them in a screw fixed to the center of the scale, allowing pressure ajdustment. The balls were made of plastic foam, painted with conductive ink. The index sticks were made from vegetal fibers used in brooms. These meters are not very precise, as the indication depends on the surroundings since they are not shielded. The size of the suspended ball essentially determines the maximum voltage that can be measured without losses, as it is there that the charge concentration is more intense, and it starts to produce corona when the voltage is greater than about 30 kV divided by the radius of the ball in cm. But they continue to work after this point, since the materials used have high resistivity. With the devices placed at the edge of a charged conductive plate, I get, for 20 kV, 90°, 60°, and 40° for the three electrometers shown, with suspended balls progressively larger. The angle initially rises in a very nonlinear way, probably effect of the base, and then becomes approximately directly proportional to the voltage, as shown below. This same effect was observed with the old electrometers too and was mentioned by Volta. The curve "P" is for the smallest electrometer, "G" for the one with guard, and #1 and #2 for two copies of the third, which should be identical but show a small difference.

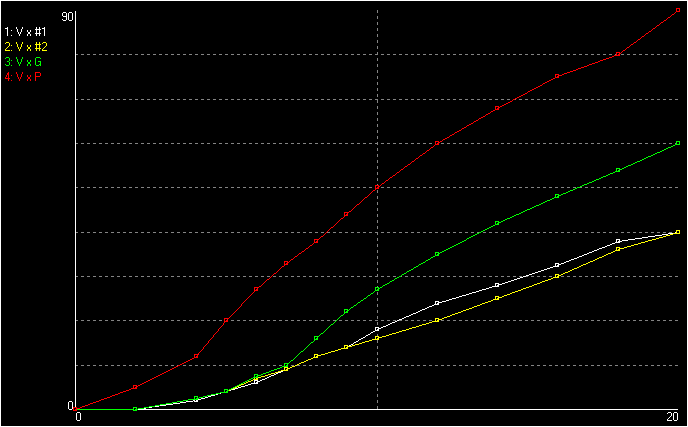Angle x voltage (kV) for the Henley electrometers.

This simple electroscope uses two plastic foam balls painted with conductive ink suspended by thin wires in an inverted acrylic cup mounted over a wood base. The upper terminal passes through a Teflon insulator in a hole in the cup, for better insulation. Two disks of adhesive aluminum foil are pasted on the interior walls of the pot and connected with the base. The top plate is made of wood. This electroscope was made as part of a "doubler of electricity", but is very useful alone. The balls separate with ~500 V, and almost touch the metal plates with ~5000 V.  The separation of the balls as function of the voltage is, approximately:

0.5 kV  0+ mm
1.0 kV  3 mm
2.0 kV  8 mm
3.0 kV 15 mm
4.0 kV 20 mm
5.0 kV Saturation

This the correct form of making a pith ball electroscope, although with modern materials, much as they were when used extensively in the early studies about electricity in the XVIII century. Better variations were the gold-leaf electroscope, invented by Bennet, where two strips of very thin gold leaf were used, that was very sensitive, and the straw electrometer, used by Volta, where two straw strips were used. The two metal strips and the conductive base are necessary, or charge accumulates on the inner walls of the cup and the balls don't close when the device is discharged. They also provide shielding from external interferences. Many modern texts show electroscopes made with a strip of aluminum foil folded over a wire inside a glass bottle. This is incorrect, and would result in a very poor instrument.

The electrometers and electroscopes can be calibrated using the spark gap, with the setup shown in the first photo, but  for verification I made a 200 MΩ resistor with 20 10-MΩ resistors connected in series, and used it in series with a microamperimeter to directly measure a test voltage, generated by a flyback-based high-voltage power supply. This method has its problems, because so high resistance is sensitive to any minimum leakage, even through the leads of the meter (when measuring the resistance) touching anything. At 20 kV there is 1000 V over each resistor (0.1 W), and they may leak or become nonlinear in this condition. The high-voltage end of the resistor string produces some corona too. I mounted the resistors over an acrylic plate strip with holes in a zigzag pattern and inserted the strip in a section of 3/4" PVC tube, with terminals at the ends for connections. The precision of the completed assembly is expected to be better than the 5% of the individual resistors, 5/√20 = 1.1%, but the actual measured value varies, depending on humidity and even on how the leads of the meter are positioned. It's better to measure all the resistors separately and add the values. Another inconvenience is that at 20 kV the resistor consumes 100 µA, a too high current for an electrostatic machine. This measurement method can then be used only to calibrate other methods.

A field-mill electric field meter can also be used. The meter is mounted at some distance from an insulated sphere, and the sphere is connected to a known low voltage with the meter in its lower range. The distance is then adjusted until an electric field with a chosen proportion to the voltage is obtained. The scale multiplier of the meter is then changed to the maximum range and high-voltage measurements can be made. For example, the sphere is connected to 15 V and the meter is adjusted to read 150 V/m at the 1 kV/m range. At the 100 kV/m range the meter reads 15 kV/m with 1.5 kV in the sphere. The problem with this system is that any high voltage present in the surroundings affects the calibration at low voltage. If the sphere is first connected to high voltage (even days before), the insulator holding it holds charge for some time, and a subsequent calibration at low voltage is affected. It's necessary to use a partially conductive support for the sphere, or to use a grounded shield around the meter and the sphere, a Faraday cage, what complicates the assembly. The calibration can of course be done without these problems by comparison with the resistor method, at high voltage, but then the precision of the first method must be asserted. Note also that the meter saturates with just 10 kV. For greater range the sphere and the meter must be quite far from each other, and calibration is more difficult, requiring greater voltage and more care with stray charges and shielding.

Calculation of the expected reading for a given voltage is possible, but the exact solution is a three-dimensions electrostatics problem. The case of the ball electroscope is well known, although without taking the metal plates or suspending wires in consideration. The case of Henley's electrometer is more complex, because the ball is repelled by a more complicated structure. 


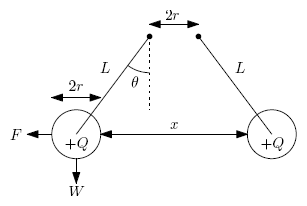
For two spheres, the angle θ with the vertical line follows the relation F/W = tan θ, with F being the electrical force in a sphere and W its weight, or gravitational force, ignoring the suspending lines. For Henley's electrometer the relation is approximately valid too, supposing that the electrical force on the sphere is horizontal. Some old instruments were graduated with tangent scales due to this [5]. The relation between the electrical force and the voltage, however, is not linear. For the pith-ball electrometer the charge in one of the balls can be easily found, assuming that the balls behave as a point charges at their centers and ignoring the suspension lines and surroundings:


where m is the mass of a ball, r the radius, x their separation, L the length of the suspension lines (to the centers of the balls), g = gravity acceleration, 9.8 m/s², and k the Coulomb constant 9 ×10⁹ Nm²/C² (1/(4πε₀) exactly, with ε₀ being the electric constant = :8.85419 × 10^-12 F/m). The voltage can be found by treating the two balls as a distributed capacitor with capacitance C and charge 2Q, resulting in V = 2Q/C. The capacitance C varies between the capacitance of two spheres in contact, 8πε₀rLn2 = 8πε₀r × 0.69315, and the capacitance of two spheres far apart, 8πε₀r. A simple approximation, with precise values for x = 0, x = 2r, and x = ∞, resulting in A = 2.50092 and B = 3.60806 (or, as in [6], A = 2 and B = 3), is:


 Instead of first finding Q and then V, the force can be found directly from the capacitance and the voltage as the derivative of the stored energy in relation to the separation of the spheres:


And then, as F = mg tan θ, a better approximation is found:


With A = 2 and B = 3 this formula gives the same result obtained by finding Q from the point charges approximation first, and works well for large distances. The exact charge, capacitance, and force can be found by series [6]. The calculations agree with experiments only approximately, because there is significant weight in the suspension lines (easy to take into account if the lines are rigid by adding m_line/2 to m), some charge too (very little), and specially because the metal plates in the walls of the electroscope and the bottom plate attract the balls. For two balls far from other objects the approximation is very good, however. For example, with two 1.5-cm plastic foam balls painted with conductive ink, m = 0.0004 kg, r = 0.0075 m, hanging with L = 0.131 m from thin lines, with V = 5 kV the separation is found experimentally as 9 mm (0.009 m). The last formula above gives V = 5.03 kV.

Old instruments


The picture above shows some measurement instruments used by Alessandro Volta. A pith ball electroscope, an electric force balance, Henley's electrometer with a guard ring, and a spark gap.